Cijferend delen, hoe doe je dat?
 Het verdelen van hoeveelheden kan best lastig zijn. Zolang het om kleinere getallen past, die we herkennen uit vermenigvuldig- en deeltafels zal het nog wel lukken. Als je geen rekenmachine in de buurt hebt, zul je papier en pen nodig om een deelsom op te lossen. Cijferend delen, met behulp van een staartdeling, hoe werkt dat?
Het verdelen van hoeveelheden kan best lastig zijn. Zolang het om kleinere getallen past, die we herkennen uit vermenigvuldig- en deeltafels zal het nog wel lukken. Als je geen rekenmachine in de buurt hebt, zul je papier en pen nodig om een deelsom op te lossen. Cijferend delen, met behulp van een staartdeling, hoe werkt dat?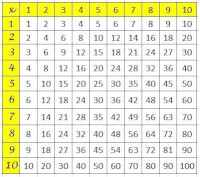 Tafel-vierkant
Tafel-vierkantVermenigvuldig- en deeltafels
Een deelsom is een omgekeerde tafelsom. Als je zegt 4 x 6 = 24, dan kun je met dezelfde getallen ook de omgekeerde som, dus een deelsom, maken, 24 : 6 = 4. Om deelsommen snel te kunnen uitrekenen is het dus van belang dat je de tafelsommen goed in je hoofd hebt zitten. Zitten de vermenigvuldigtafels in je hoofd, dan zullen de deeltafels minder een probleem zijn. Als je het nog niet allemaal goed in je hoofd hebt, kun je bij het uitrekenen van deelsommen eventueel gebruik maken van een tafel-vierkant, waarin je alle uitkomsten van de tafeltjes van 1 t/m 10 ziet staan. Maak je gebruik van zo’n tafelvierkant, wen je dan aan om elke keer als je een uitkomst opzoekt ook de hele som te zeggen. Op die manier leer je ze uiteindelijk toch beter onthouden.Maar als het moeilijk wordt
Zeker met grotere en complexere getallen gaat het uit het hoofd niet meer lukken, dan heb je speciale technieken nodig om de oplossing van een deelsom te vinden. Cijferend delen kan op twee manieren. Ofwel met een verdeelschema in een kolomvorm, ofwel door het maken van een staartdeling.Cijferend delen: een verdeelschema
 Opzetten van het verdeelschema
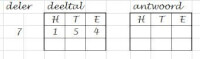
Opzetten van het verdeelschema- Allereerst teken je, liefst met een liniaal, een schema, zoals je hiernaast in de afbeelding zit. Je ziet dat de tweede kolom weer is onderverdeeld in een kolom voor duizendtallen, honderdtallen, tientallen en eenheden. Deze onderverdeling is niet noodzakelijk, maar maakt het wel duidelijker. Bovendien kun je, door de cijfers steeds in de juiste subkolom te schrijven, het maken van slordigheidsfouten voorkomen. Ook de derde kolom heeft zo’n onderverdeling.
- De deler, het getal waar je door deelt, schrijf je in de eerste kolom. Het deeltal, dat is het getal dat je wilt verdelen, komt in de tweede kolom. In de derde kolom komen de deelantwoorden en het uiteindelijke antwoord. We bekijken de som 154 : 7, zoals je ziet zijn deze getallen in het voorbeeld hiernaast al ingevuld.
- Je kijkt naar de som. Hoe vaak zou je 7 van de 154 af kunnen halen? Zou het 10 keer gaan? Laten we dat eens proberen.
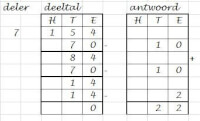
- 10 keer 7, dat is 70. Je haalt dus 70 van de 154 af. Zet de 0 onder de 4 in de kolom van de eenheden, de 7 komt onder de 5 van de tientallen. Reken de aftreksom 154 – 70 uit. Het antwoord is 84. In de kolom van de deelantwoorden schrijf je 10 in de juiste kolommen, je hebt immers 10 keer 7 van de 154 afgehaald.
- Je kijkt naar de hoeveelheid die je nu over hebt. 84. Hoe vaak zou hier 7 van afkunnen? Zeker nog wel 10 keer, want 10 x 7 = 70, en dat past prima in de 84. Noteer 70 weer onder de 84 en reken de aftreksom uit. Je houdt 14 over. In de kolom van het antwoord noteer je ook deze 10.
- Je kijkt naar de hoeveelheid die je nu over hebt, 14. Daar past 7 precies 2 keer in, want dat is 14. Noteer de 14 en reken de aftreksom uit. De uitkomst is, het zal je niet verbazen, 0. In de kolom van het antwoord zet je 2.
- Nu tel je alle deelantwoorden bij elkaar op: 10 + 10 + 2 = 22. De uitkomst van de deling 154 : 7 is dus 22.
Je ziet, het werkt prima. Het nadeel van deze methode is dat je relatief veel schrijft en veel papier gebruikt om één enkele som uit te rekenen. Je zult in het hoofdstuk De staartdeling zien dat het wel wat vlugger en met minder papier kan.
Cijferend delen: de staartdeling
De staartdeling is een stuk sneller, maar het vraagt wel wat van je:- Nauwkeurig werken
- Je moet de tafeltjes goed kennen
- Je moet snel vermenigvuldigingen kunnen maken, uit het hoofd of soms ook cijferend.
We gaan weer uit van dezelfde som: 154 : 7.
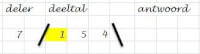 Opzetten van de staartdeling
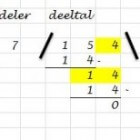
Opzetten van de staartdeling- Eerst schrijf je 7, daarna een voorwaartse schuine streep. (Op de computer zou je zo’n streep een slash noemen.) Nu volgt het deeltal, 154. Je sluit af met een achterwaartse schuine streep. (Op de computer zou je dit een backslash noemen.) Achter de laatste schuine streep is ruimte voor het antwoord.
- Je kijkt naar het eerste cijfer van het deeltal, de 1. Je stelt je de vraag of je dit kunt delen door de deler (7). Het antwoord is natuurlijk: nee. We gaan verder met de volgende stap.
- Omdat je het eerste cijfer niet kon delen door de deler, gaan we nu verder met de eerste twéé cijfers van het deeltal. Dat is 15. Kun je dit delen door 7? Het antwoord is ja. Nu is nog de vraag: hoe vaak. Omdat je de tafel van 7 natuurlijk goed kent, zie je meteen dat het zeker 2 keer kan, want 2 x 7 = 14. Je noteert de 14 onder de 15 en zet achter de laatste schuine streep 2.
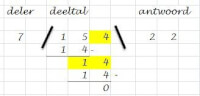
- Je trekt 14 van 15 af. Het antwoord is 1. Je vraagt je af of je 1 door 7 kunt delen. Nee.
- Kijk naar het volgende cijfer in het deeltal. Dat is 4. Die 4 ‘haal’ je naar beneden. Soms wordt gezegd: “Je haalt de 4 aan.” Je schrijf de 4 achter de 1. Nu staat er 14. Je ziet meteen, dat je dat prima door 7 kunt delen, dat gaat 2 keer, 2 x 7 = 14. Je noteert deze 14 onder de 14, en rekent de aftreksom uit. Antwoord is natuurlijk 0. Omdat je weer 2 keer kon verdelen, schrijf je aan de antwoordkant een 2 achter het vorige gevonden cijfer, ook een 2.
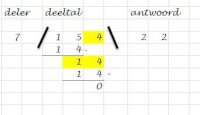
- Je ziet nu het antwoord staan: 22.
En als het nou niet uitkomt?
In het vorige voorbeeld kwam de som precies uit. Je kunt je voorstellen, dat dit niet altijd lukt. Wat je overhoudt is dan de rest. Soms moet je die achter het antwoord schrijven. In het voorbeeld hierboven zou dat zijn 22 rest 0. (Maar omdat de rest 0 is, schrijf je dat eigenlijk bijna nooit zo op.) In het volgende voorbeeld is de rest geen 0. Staartdeling met rest
Staartdeling met rest- Noteer de opgave 81 : 10
- Kijk naar het eerste cijfer van het deeltal, 8. Dat kun je niet door 10 delen, dus je gaat verder.
- Kijk naar de eerste twee cijfers van het deeltal, 81. Dat kun je door 10 delen. Het gaat 8 keer, want 8 x 10 = 80. Je noteert 80 onder de 81, en rekent de aftreksom uit. Het antwoord is 1. Je noteert 8 aan de antwoordkant, want het ging 8 keer.
- Er is geen volgend cijfer in het deeltal, je hebt ze allebei al gehad. Je kunt dus niet verder, je blijft met 1 zitten dat nog niet is verdeeld. Je antwoord is 8, rest 1.
Achter de komma
Een deling waar een antwoord met rest uitkomt is niet altijd handig, soms moet het nog nauwkeuriger. Dat kan door ‘achter de komma’ verder te gaan, je krijgt dan een decimale breuk als antwoord. Kijk naar het volgende voorbeeld, 100 : 8
- Noteer de opgave 100 : 8
- Kijk naar het eerste cijfer van het deeltal, 1. Dat kun je niet door 8 delen, we gaan verder.
- Kijk naar de eerste twee cijfers van het deeltal, 10. Dat kun je door 8 delen, het gaat 1 keer. Noteer de 1 aan de antwoordkant en zet 8 onder de 10. Maak de aftreksom. Je houdt 2 over.
- Haal het volgende cijfer van het deeltal aan, een 0, en schrijf deze achter de 2. Je hebt nu 20. Dat kun je door 8 delen. Het gaat 2 keer, want 2 x 8 = 16. Schrijf de 2 achter de 1 van het antwoord, en 16 onder de 20. Reken de aftreksom uit. Je houdt 4 over.

- Er zijn geen volgende cijfers meer in het deeltal. Je antwoord zou kunnen zijn 12, rest 4. Maar het moet preciezer. We doen net alsof er achter het deeltal nog een komma staat en een 0. Het deeltal wordt dan 100,0. Nu kunnen we wél ets aanhalen. Je komt eerst een komma tegen. Schrijf daarom nu eerst een komma achter het antwoord. Haal nu de 0 aan, en schrijf deze achter de 4. Nu staat er 40. Aangezien 5 x 8 = 40 weet je dat 8 nog 5 keer in 40 past. Schrijf de 5 achter de komma van het antwoord, de 40 onder de 40. Reken de aftreksom uit, er komt natuurlijk 0 uit.
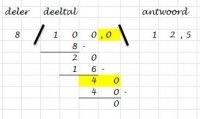
- Je hebt het antwoord gevonden. 12,5.