Cijferend aftrekken, hoe doe je dat?

Het van elkaar aftrekken van kleinere getallen, bijvoorbeeld onder de 10 of onder de 100 is meestal niet zo moeilijk, en kun je uit het hoofd. Gaat het om meerdere getallen, of zijn de getallen net wat groter, dan wordt het lastiger en hebben we een andere techniek nodig, het cijferend aftrekken. Cijferend aftrekken, hoe doe je dat?

Eenvoudige opgaven, snel gedaan

Het is meestal niet zo'n probleem om simpele opgaven uit het hoofd uit te rekenen. De antwoorden op simpele vraagstukken diep je in de meeste gevallen uit je geheugen op, je hebt dit soort opgaven geautomatiseerd. Over een opgave als 6 - 2 of 12 - 2 hoef je niet lang na te denken, het antwoord staat je als vanzelf helder voor de geest. Met grotere getallen wordt het een ander verhaal. Het geheugen heeft geen direct antwoord voor je klaarstaan, maar door strategieën toe te passen kun je nog een heel eind komen. Zo kun je een opgave als 51 - 26 toch wel oplossen. Je begin bijvoorbeeld met 50 - 26, en telt bij de uitkomst vervolgens nog 1 op. Of je trekt eerst de tientallen af, 51 – 20 = 31, dan haal je vervolgens de eenheden er af: 31 – 6 = 25.

Het wordt lastig met grotere getallen

Op een gegeven moment worden de getallen te groot. Dat redt je niet meer met je geheugen of met simpele strategieën. Gelukkig zijn er oplossingen om, zonder rekenmachine, aftreksommen cijferend uit te rekenen. Er zijn twee mogelijkheden:

Kolomrekenen, waarbij je van rechts naar links of juist van links naar rechts werkt.
Onder elkaar cijferend aftrekken, waarbij soms een waarde geleend moet worden.

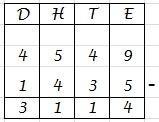
Een opgave als 4549 - 1435 kun je met elk van deze mogelijkheden oplossen. Hieronder kun je zien hoe dat in zijn werk gaat. Let er bij het noteren van getallen altijd op, dat je de eenheden, tientallen, honderdtallen en duizendtallen bij elkaar houdt. Zo schrijf je eenheden altijd onder eenheden, tientallen altijd onder tientallen, en ga zo maar door. Als je dit niet doet, dan gaan de berekeningen fout.

Van links naar rechts.

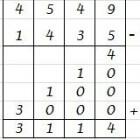
Aftrekken door kolomrekenen, van links naar rechts

Je trekt om te beginnen de duizendtallen van elkaar af, dus 4000 - 1000. De uitkomst, 3000 noteer je in het schema.
Nu haal je de honderdtallen van elkaar af, 500 - 400. De uitkomst 100 komt onder de vorige uitkomst te staan.
Nu zijn de tientallen aan de beurt, 40 - 30. De uitkomst 10 schrijf je weer onder de vorige uitkomst.
Nu trek je de eenheden van elkaar af, 9 - 5. Schrijf de uitkomst 4 weer onder de vorige uitkomst.
Nu tel je alle deeluitkomsten bij elkaar op, en dat levert je de uitkomst 3114 op.

Van rechts naar links

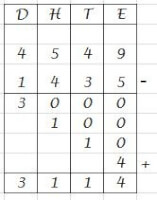
Aftrekken door kolomrekenen, van rechts naar links

Het kolomrekenen van rechts naar links lijkt erg op de variant van links naar rechts, alleen de werkvolgorde is precies andersom. Als je van rechts naar links werkt, begin je bij de laagste waardes, de eenheden. Daarna komen de tientallen, dan de honderdtallen en daarna de duizendtallen. En daarna de eventuele grotere waardes, natuurlijk. De tussenuitkomsten noteer je zoals je in het voorbeeld hiernaast ziet.

Onder elkaar aftrekken, waarbij nog even geen waarde geleend moet worden

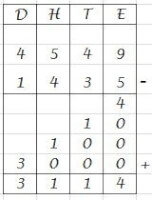
Cijferend aftrekken, er hoeft nog niet geleend te worden

Wil je liever wat minder schrijven en sneller de sommen af hebben dan bij kolomrekenen? Dan zit je bij deze vorm van cijferend optellen goed. Je moet er wel je aandacht en je geheugen goed bij houden, want daar wordt wel meer een beroep op gedaan. We gaan weer uit van dezelfde som, 4549 – 1435.

We beginnen bij de eenheden: 9 – 5 = 4. Schrijf de 4 onder de eenheden.
Nu de tientallen: 4 – 3 = 1. Schrijf de 1 onder de tientallen.
De honderdtallen: 5 – 4 = 1. Je noteert de 1 onder de honderdtallen.
De duizendtallen: 4 – 1 = 3. Zet de 3 onder de duizendtallen.
De uitkomst is gevonden: 3114

Onder elkaar aftrekken, waarbij geleend moet worden.

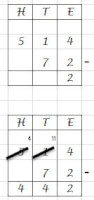Cijferend aftrekken, er moet geleend worden

Soms kom je bij het uitvoeren van een deel van de opgave voor een probleem te staan, je komt tekort. Laten we eens kijken wat er aan de hand kan zijn, en hoe je dat cijferend kunt oplossen: door te lenen. We gaan de som 514 – 72 uitrekenen.

Allereerst worden de cijfers netjes onder elkaar geschreven.
We beginnen met de eenheden. 4 – 2 = 2. Noteer de 2 onder de eenheden.
Nu de tientallen. 1 – 7 =…. Probleem! Je kunt geen 7 van de 1 afhalen! We lossen dat op door naar de honderdtallen te kijken, daar staan er 5. We lenen één van die honderdtallen, strepen de 5 weg en maken er een 4 van. Het honderdtal dat we hebben gepakt is eigenlijk 10 tientallen. Dat tellen we bij de tientallen die we al hadden, 1 + 10 = 11. We strepen de 1 bij de tientallen weg en maken er een 11 van. Nu kan de opgave verder worden uitgerekend. 11 – 7 = 4. Noteer de 4 onder de tientallen.
Nu de honderdtallen. We hebben nog 4 honderdtallen over. Er onder staat niets, er hoeft dus niets van af. We noteren een 4 onder de honderdtallen.
De uitkomst is gevonden: 442

Grotere getallen

Ook met grotere getallen zul je regelmatig moeten lenen bij de naast-hogere waarde om de aftrekopgave uit te rekenen. Het kan dus voorkomen, dat je bij elke tussenstap zult moeten lenen, bijvoorbeeld bij een opgave als 2222 - 333.