Cijferend optellen, hoe doe je dat?
 Het komt regelmatig voor dat je getallen bij elkaar moet tellen. Zo lang het om kleine getallen gaat, bijvoorbeeld onder de 10 of onder de 100 lukt het nog aardig om dat uit het hoofd te doen. Gaat het om méér dan twee getallen, of om grotere getallen, dan hebben we vaak een hulpmiddel nodig. Dat is er: we kunnen cijferend optellen. Cijferend optellen, hoe doe je dat?
Het komt regelmatig voor dat je getallen bij elkaar moet tellen. Zo lang het om kleine getallen gaat, bijvoorbeeld onder de 10 of onder de 100 lukt het nog aardig om dat uit het hoofd te doen. Gaat het om méér dan twee getallen, of om grotere getallen, dan hebben we vaak een hulpmiddel nodig. Dat is er: we kunnen cijferend optellen. Cijferend optellen, hoe doe je dat?Uit het hoofd
Eenvoudige sommen reken je gewoon uit je hoofd uit. Veel ervan ken je zelfs van buiten. Erbij-sommen als 5 + 5 of 15 + 5, daar draai je je hand niet voor om. De uitkomst heb je bijna meteen in je hoofd, het kost je nauwelijks moeite. Naar mate de getallen groter worden kun je er niet meer op vertrouwen dat de uitkomst ‘als vanzelf’ in je opkomt. Met verschillende optelstrategieën los je een opgave als 25 + 26 toch wel op. Je bedenkt bijvoorbeeld dat je eerst 25 + 25 uitrekent, en vervolgens nog 1 bij de uitkomst telt. Of je doet eerst de tientallen bij elkaar, 20 + 20, dan de eenheden 5 + 6, en vervolgens de beide uitkomsten bij elkaar 40 + 11 = 51.Cijferend optellen met grotere getallen
Als de getallen wat groter worden, kun je het meestal niet meer uit je hoofd. Met de optelstrategieën zou het nog kunnen lukken, maar omdat er teveel tussenstappen komen loop je meer risico dat je iets vergeet. Naarmate de getallen om op te tellen groter worden, of het aantal op te tellen getallen toeneemt, wordt de kans op fouten ook groter. Gelukkig zijn er oplossingen om, zonder rekenmachine, optellingen cijferend uit te voeren. Er zijn drie mogelijkheden:- Kolomrekenen, van rechts naar links
- Kolomrekenen, van links naar rechts
- Onder elkaar optellen, waarbij soms een waarde onthouden moet worden.
Laten we eens bekijken hoe je met deze mogelijkheden een optelling als 4544+ 1435 uitrekent. Welke vorm je ook kiest, het is erg belangrijk dat je de juiste cijfers onder elkaar hebt staan. Eenheden staan onder eenheden, tientallen onder tientallen, honderdtallen onder honderdtallen en de duizendtallen onder de duizendtallen. Doe je dit niet zorgvuldig, dan is de kans op fouten erg groot.
Kolomrekenen, van links naar rechts
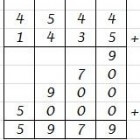
 Optellen door kolomrekenen, van links naar rechts
Optellen door kolomrekenen, van links naar rechts- Je telt allereerst de duizendtallen bij elkaar, dus 4000 + 1000. De uitkomst, 5000, schrijf je op.
- Nu tel je de honderdtallen bij elkaar, 500 + 400. De uitkomst 900 schrijf je op onder de vorige uitkomst.
- Nu zijn de tientallen aan de beurt, 40 + 30. De uitkomst 70 komt weer onder de vorige uitkomst.
- Als laatste tel je nu de eenheden bij elkaar, 4 + 5. De uitkomst 9 komt er weer onder te staan.
- De tussenstappen zijn gezet, nu tel je de delen van de uitkomst bij elkaar op, zodat je de uitkomst 5979 krijgt.
Je ziet dat je met deze werkwijze een vorm van een kolom oplevert op je uitrekenpapier, vandaar de naam.
Kolomrekenen, van rechts naar links
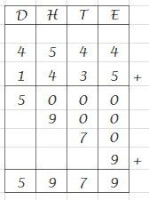
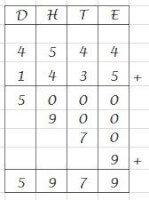 Optellen door kolomrekenen, van rechts naar links
Optellen door kolomrekenen, van rechts naar linksOnder elkaar optellen, waarbij nog even geen waarde onthouden moet worden
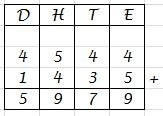 Onder elkaar optellen
Onder elkaar optellen- Allereerst kijk je in de kolom van de eenheden. Je telt ze bij elkaar: 4 + 5 = 9. Noteer de 9 onder de eenheden.
- Dan tel je de tientallen bij elkaar: 4 + 3 = 7. Noteer een 7 onder de tientallen.
- Dan tel je de honderdtallen bij elkaar: 5 + 4 = 9. Noteer een 9 onder de honderdtallen.
- Als laatste komen de duizendtallen: 4 + 1 = 5. Noteer een 5 onder de duizendtallen.
- Je ziet de uitkomst 5979 staan.
Onder elkaar optellen, waarbij onthouden moet worden
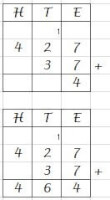 Onder elkaar optellen, waarbij onthouden moet worden
Onder elkaar optellen, waarbij onthouden moet wordenNoteer de getallen goed onder elkaar, eenheden onder eenheden, tientallen onder tientallen.
We beginnen weer bij de eenheden. 7 + 7 = 14. Je noteert de eenheden van dit antwoord, 4, onder de eenheden. Je houdt één tiental over, die onthoud je even. Je noteert heel klein een 1 boven de tientallen, als geheugensteuntje dat je nog één tiental in je vervolgberekening moet meenemen.
Nu tel je de tientallen bij elkaar, 2 + 3 = 5. Maar let op, je had één tiental onthouden, dus die moet je er nog bijtellen: 5 + 1 = 6. Je noteert de 6 onder de tientallen.
Nu zijn de honderdtallen aan de beurt. Je hebt 4, eronder staat niets, dus 0. Dat wordt dus 4 + 0 = 4. Je noteert een 4 onder de honderdtallen en krijgt de uitkomst van de opgave, 464.
Een tikkeltje moeilijker optellen met onthouden
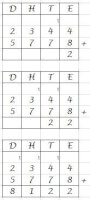 Onder elkaar optellen met grotere getallen
Onder elkaar optellen met grotere getallenEerst de eenheden, 4 + 8 = 12. Je noteert een 2 bij de tientallen, en onthoudt één tiental.
De tientallen, 4 + 7 = 11, maar daar komt het ene onthouden tiental bij: 11 + 1 = 12. Je noteert een 2 bij de tientallen en onthoudt één honderdtal.
De honderdtallen, 3 + 7 = 10, maar daar komt het ene onthouden honderdtal bij: 10 + 1 = 11. Je noteert een 1 bij de honderdtallen en onthoudt één duizendtal.
De duizendtallen, 2 + 5 = 7, maar daar komt het ene onthouden duizendtal bij: 7 + 1 = 8. Je noteert een 8 bij de duizendtallen.
Je uitkomst is klaar: 8122
Meerdere getallen
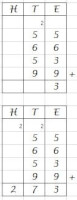 Onder elkaar optellen van meerdere getallen
Onder elkaar optellen van meerdere getallenJe noteert alles weer netjes onder elkaar.
Je begint bij de eenheden: 5 + 6 + 3 + 9 = 23. Je noteert een 3 bij de eenheden, en onthoudt twéé tientallen.
Dan de tientallen 5 + 6 + 5 + 9 = 25, maar daar komen de twee onthouden tientallen bij: 25 + 2 = 27. Je noteert een 7 bij de tientallen.
Je hebt nog twee honderdtallen over. Omdat je in de som geen honderdtallen hebt, heb je nu eigenlijk een som als 0 + 0 + 0 + 0 + 2. Ofwel, je noteert de 2 bij de honderdtallen en je hebt de uitkomst 253.