Cijferend vermenigvuldigen, hoe doe je dat?
 Je hebt niet altijd een rekenmachine nodig om bepaalde rekenopgaven op te lossen. Maar uit het hoofd lukt het ook niet altijd. De tafels van vermenigvuldiging zullen we meestal uit het hoofd kennen, maar voor keersommen, het vermenigvuldigen van grotere getallen, gebruiken we het cijferend vermenigvuldigen. Cijferend vermenigvuldigen, hoe doe je dat?
Je hebt niet altijd een rekenmachine nodig om bepaalde rekenopgaven op te lossen. Maar uit het hoofd lukt het ook niet altijd. De tafels van vermenigvuldiging zullen we meestal uit het hoofd kennen, maar voor keersommen, het vermenigvuldigen van grotere getallen, gebruiken we het cijferend vermenigvuldigen. Cijferend vermenigvuldigen, hoe doe je dat?
Herhaald optellen
In plaats van vermenigvuldigingen wordt op scholen ook veel gebruik gemaakt van de term keersommen. Het deelwoordje keer komt in een keersom dan ook als vast element voor. Vermenigvuldigen is eigenlijk een vorm van herhaald optellen. De som 3 x 5 spreek je uit als drie keer vijf. En vertaald is dat: één keer vijf, nóg een keer vijf en nóg een keer vijf. Ofwel: 5 + 5 + 5. Weet je de opgave 3 x 5 niet meteen uit je hoofd, dan kun je er via de optelling nog achter komen. 5 + 5 + 5 = 15.
Tafels van vermenigvuldiging
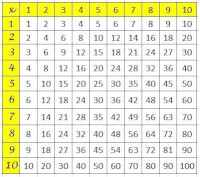
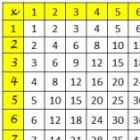
Tafelkaart met alle uitkomsten van de tafeltjes.
Complex
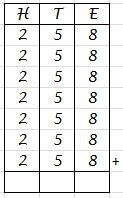
Zo'n lange som, dat schrikt toch af!
Cijferend vermenigvuldigen, de langere manier
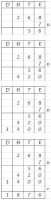
Cijferend vermenigvuldigen, de lange manier
- Let er altijd op dat eenheden netjes onder eenheden staan, tientallen onder tientallen, honderdtallen onder honderdtallen, enzovoort.
- We beginnen bij de eenheden. Boven staat 8, daaronder staat 7x. Je rekent dus uit: 7 x 8 = 56. Noteer 56, waarbij de 6 onder de eenheden komt, de 5 onder de tientallen.
- We gaan door met de tientallen. Boven staat een 6, dat is dus eigenlijk 60, daaronder 7x. Je rekent dus uit: 7 x 60 = 420. Noteer 420, waarbij de 0 onder de eenheden komt, de 2 onder de tientallen en de 4 onder de honderdtallen.
- We gaan door me de honderdtallen. Boven staat een 2, dat is dus eigenlijk 200, daaronder staat 7x. Je rekent dus uit: 7 x 200 = 1400. Noteer 1400, waarbij er een 0 bij de eenheden, een 0 bij de tientallen, een 4 bij de honderdtallen en een 1 bij de duizendtallen komt te staan.
- Je telt de tussenuitkomsten bij elkaar op. 56 + 420 + 1400. Dat doe je door gebruik te maken van het cijferend optellen. De uitkomst is 1876.
Cijferend vermenigvuldigen, de kortere manier
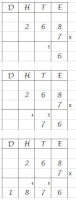
Cijferend vermenigvuldigen, de kortere manier
- We nemen weer 7 x 268. Noteer 268 en daaronder 7x. Let er weer op dat eenheden, tientallen en honderdtallen netjes onder elkaar komen te staan.
- We beginnen bij de eenheden, 7 x 8 = 56. Noteer een 6 bij de eenheden, en de 5 moet je even onthouden. Je kunt eventueel die 5 heel klein even bij de tientallen zetten.
- Nu de tientallen, 7 x 6 = 42. Daar komen de 5 bij die je had onthouden, dus 42 + 5 = 47. Noteer de 7 onder de tientallen, de 4 moet weer worden onthouden. Je kunt eventueel die 4 heel klein even bij de honderdtallen zetten.
- Nu de honderdtallen, 7 x 2 = 14. Daar komen weer de 4 bij die je had onthouden, dus 14 + 4 = 18. De 8 noteer je bij de honderdtallen, de 1 komt bij de duizendtallen.
- Je ziet het antwoord staan: 1876
We maken het moeilijker
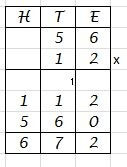
Vermenigvuldigen met grotere getallen
- Allereerst schrijf je de som op, waarbij je er weer op let dat eenheden en tientallen netjes onder elkaar komen te staan.
- We vermenigvuldigen met 12. Dat is te lastig in één keer, dus we gaan het in twee stappen doen: eerst de eenheden (dus: 2), daarna de tientallen (dus: 1).
- We vermenigvuldigen met 2. Eerst de eenheden, dus 2 x 6 = 12. Noteer 12, waarbij de 2 onder de eenheden komt, de 1 moet je even onthouden of je zet een 1 in het klein onder de tientallen.
- We vermenigvuldigen nog steeds met de 2, nu zijn de tientallen aan de beurt, dus 2 x 5 = 10. Daar komt de 1 bij die je onthouden had, dus 11. Noteer 11, waarbij de 1 onder de tientallen komt en de 1 onder de honderdtallen.
- Klaar met vermenigvuldigen met de 2, dus we gaan met de tientallen vermenigvuldigen. Als je met een tiental vermenigvuldigd zijn er in de uitkomst geen eenheden, dus je schrijft een 0 onder de eenheden.
- We vermenigvuldigen met de 1 van de tientallen. We beginnen met de eenheden, dus 1 x 6 = 6. Noteer een 6 onder de tientallen.
- We vermenigvuldigen met de 1 van de tientallen. We gaan naar de tientallen, dus 1 x 5 = 5. Noteer een 5 onder de honderdtallen.
- Je ziet nu twee uitkomsten staan, 112 als uitkomst van 2 x 56, en daaronder 560 als uitkomst van 10 x 56.
- Die twee uitkomsten tel je cijferend bij elkaar op. De uitkomst is 672.
 Je hebt niet altijd een rekenmachine nodig om bepaalde rekenopgaven op te lossen. Maar uit het hoofd lukt het ook niet altijd. De tafels van vermenigvuldiging zullen we meestal uit het hoofd kennen, maar voor keersommen, het vermenigvuldigen van grotere getallen, gebruiken we het cijferend vermenigvuldigen. Cijferend vermenigvuldigen, hoe doe je dat?
Je hebt niet altijd een rekenmachine nodig om bepaalde rekenopgaven op te lossen. Maar uit het hoofd lukt het ook niet altijd. De tafels van vermenigvuldiging zullen we meestal uit het hoofd kennen, maar voor keersommen, het vermenigvuldigen van grotere getallen, gebruiken we het cijferend vermenigvuldigen. Cijferend vermenigvuldigen, hoe doe je dat? Tafelkaart met alle uitkomsten van de tafeltjes.
Tafelkaart met alle uitkomsten van de tafeltjes. Zo'n lange som, dat schrikt toch af!
Zo'n lange som, dat schrikt toch af! Cijferend vermenigvuldigen, de lange manier
Cijferend vermenigvuldigen, de lange manier Cijferend vermenigvuldigen, de kortere manier
Cijferend vermenigvuldigen, de kortere manier Vermenigvuldigen met grotere getallen
Vermenigvuldigen met grotere getallen