De kunst van het cijferen
Bewerkingen onder de 100 reken je over het algemeen uit je hoofd uit. Als je de structuur van tientallen en eenheden doorziet, weet je ook opgaven als 48 + 37 eenvoudig uit het hoofd uit te rekenen. Bij het vermenigvuldigen, in feite een herhaald optellen, leer je tafelsommen onder de 100 uit je hoofd. En dat maakt het maken van deelsommen weer gemakkelijk. Maar hoe werkt het met grotere getallen?Het begin
In de lage klassen van de basisschool wordt je ingewijd in de geheimen van getallen en bewerkingen. Je leert omgaan met rekentaal, je leert te tellen en je leert dat aan hoeveelheden getallen kunnen worden gehangen. Je leert het verschil tussen meer en minder. Dan leer je ook hoe je getallen kunt manipuleren, hoe je hoeveelheden bij elkaar of van elkaar af kunt halen. Zonder deze basisvaardigheden loop je een achterstand op, de macht van het getal is groot.Sommen maken
Er zijn verschillende bewerkingen mogelijk met getallen, je kunt verschillende soorten sommen maken.- Als je hoeveelheden bij elkaar doet, maak je een optelopgave, of een erbij-som.
- Als je dezelfde hoeveelheid vaker optelt, ben je bezig met een herhaalde optelling, ofwel: een vermenigvuldiging.
- Als je hoeveelheden van elkaar afhaalt, maak je een aftreksom, of een eraf-som.
- Wanneer je dezelfde hoeveelheid vaker van een getal afhaalt, ben je bezig met een herhaalde eraf-opgave, ofwel: een deling.
Er zijn meer bewerkingen denkbaar, maar de basisschool beperkt zich over het algemeen tot de bovenstaande.
Uit het hoofd optellen, aftrekken, vermenigvuldigen en delen
Zeker opgaven onder de twintig leer je snel uit je hoofd uit te rekenen. In feite leer je deze opgaven uit je hoofd. Bij een opgave als 13 + 5 hoef je nauwelijks meer na te denken. De uitkomst 18 komt als vanzelf bij je op. Bij grotere getallen heb je geleerd welke strategie je moet gebruiken. De combinatie van hetgeen je uit je hoofd weet en die strategie maakt dat je bijna altijd met het juiste antwoord op de proppen komt. Bij getallen boven de 100 wordt dat lastiger, het aantal deelstappen dat je bij het uit het hoofd uitrekenen moet onthouden maakt de kans op fouten groter. Gelukkig is daar iets op gevonden: het cijferend rekenen.Cijferen
Bij het cijferen, ofwel het cijferend rekenen, maken we gebruik van eenvoudige hulpmiddelen: pen en papier. Elke bewerking heeft zijn eigen methode, dus met een viertal methodes kun je alle gangbare cijfersommen uitrekenen, optellen, aftrekken, vermenigvuldigen en delen. In principe maakt de grootte van het getal niet meer uit. Dit alles is mogelijk dankzij de manier waarop ons getalsysteem in elkaar zit, een decimaal positiestelsel.Basis van het moderne rekenen: het positiestelsel
In de vroege menselijke cultuurgeschiedenis werden hoeveelheden geteld door het plaatsen van streepjes of kerfjes. Dat werkt prima met kleinere hoeveelheden, maar is erg onhandig als je tientallen of honderdtallen wilt weergeven. Daarom werden hoeveelheden gegroepeerd. Je ziet dit terug in ons huidige decimale getalstelsel: voor elke tien eenheden kun je ook één tiental pakken, voor elke tien tientallen neem je één honderdtal, en zo kun je doorgaan. Bovendien is precies afgesproken in welke volgorde die elementen worden genoteerd: van links naar rechts schrijven we van groot naar klein. Als we de letter E voor de eenheden nemen, de letter T voor tientallen, de letter H voor honderdtallen en de D voor duizendtallen, dan schrijf je dus DHTE. In cijfers: een getal als Twaalfhonderd-éénendertig schrijf je als 1231. Eén duizendtal, twee honderdtallen, drie tientallen en één losse eenheid. Zitten er in een getal bijvoorbeeld geen tientallen, zoals in twaalfhonderd-één, dan schrijf je op de plaats van de tientallen een 0, dus 1201. Het decimale stelsel, in combinatie met het exact voorgeschreven positiestelsel maakt het mogelijk om met eenvoudige methodes rekenopgaven cijferend uit te rekenen.Vormen van cijferend rekenen
We onderscheiden vier vormen van cijferend rekenen:- Cijferend optellen
- Cijferend aftrekken
- Cijferend vermenigvuldigen
- Cijferend delen
Binnen elke vorm zijn weer variaties in de gebruikte methode of wijze van noteren mogelijk, maar de uitkomst is bij elke variatie uiteraard hetzelfde.
Voorbeelden
Hier zie je enkele afbeeldingen van cijfersommen.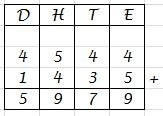 Cijferend optellen
Cijferend optellen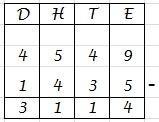 Cijferend afrekken
Cijferend afrekken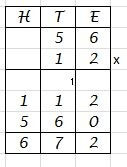 Cijferend vermenigvuldigen
Cijferend vermenigvuldigen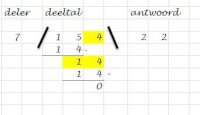 Cijferend delen, de staartdeling
Cijferend delen, de staartdeling