Rekenen met procenten, hoe doe je dat?

Elke dag worden we geconfronteerd met procenten. Is het niet via het nieuws of via statistieken in diverse media, dan is het wel omdat allerlei mensen ons verzekeren dat ze iets voor de volle honderd of tweehonderd procent doen. Of in de winkel, waar we getrakteerd worden op vette kortingen van een aantal procent. Waar hebben we het eigenlijk over als we procenten gebruiken. Rekenen met procenten, hoe doe je dat?

Populaire procenten

Procenten worden veel gebruikt. Winkels prijzen ons kortingen aan van vele procenten. Natuurlijk hoopt men dat we hierdoor verleid worden tot een aankoop. De nieuwslezer vertelt ons, dat het aantal stemmers op een bepaalde partij met wel tien procent is gestegen of gedaald. Of in statistieken zie je een bepaald percentage stijging van verkopen, gebeurtenissen en noem maar op. Een percentage klinkt soms niet zo duidelijk, waar hebben we het eigenlijk over? Hoe goed we procenten snappen hoor je aan uitspraken als ‘Ik geef alles wat ik heb, ik ga er voor de volle tweehonderd procent voor’. Kan dat eigenlijk wel? Laten we eens kijken waar we het eigenlijk over hebben.

Eén procent

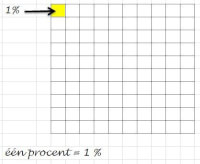1 % is één van de honderd

De letterlijke betekenis van één procent is: één van de honderd. Heb je honderd knikkers, dan is één knikker dus één procent van al je knikkers.
Heb je tweehonderd knikkers, dan is één procent twéé knikkers. Eén procent betekent immers ‘één voor elke honderd’. Je hebt twee keer honderd, en voor elke honderd één knikker maakt samen twee knikkers.
Het is een beetje lang om elke keer ‘één procent‘ te schrijven. In plaats van een geschreven getal gebruiken we liever een gewoon getal. In plaats van het woord ‘procent’ gebruiken we een symbool: %. Dat betekent dat we één procent kunnen gaan schrijven als 1 %. Dat schrijft een stuk sneller en gemakkelijker!
Uiteraard kun je meer dan één procent hebben. Als één procent betekent dat je 1 hebt op 100, dan betekent 2 procent dat je 2 van de honderd hebt. En 5 % is dan 5 van de honderd.

Een paar voorbeelden op een rijtje

1 % van 100 = 1
2 % van 100 = 2
3 % van 100 = 3
5 % van 100 = 5
10 % van 100 = 10

Verschillende hoeveelheden

Je hebt meestal andere hoeveelheden dan precies 100. Dat betekent:

1 % van 100 = 1
1 % van 50 = ½
1 % van 200 = 2
1 % van 500 = 5

Verschillende percentages, verschillende hoeveelheden

Bovenstaande voorbeelden gaan steeds over 1 % van wisselende hoeveelheden, of verschillende percentages van 100. In de praktijk wisselen percentages en hoeveelheden, zoals in dit rijtje voorbeelden.

1 % van 100 = 1
1 % van 500 = 5
2 % van 500 = 10
5 % van 500 = 25
10 % van 500 = 50
15 % van 500 = 75

Percentages en breuken

Zoals je hebt gezien, één procent is ‘een van de honderd’, ofwel het één-honderdste deel. Dat kun je ook in een breuk opschrijven, zoals je hiernaast in het plaatje ziet.
Op dezelfde manier kun je 5 %, 10 %, 25 %, 50 % en natuurlijk élk denkbaar percentage in een breuknotatie zetten. Let op 5 % is niet hetzelfde als vijf-honderdsten, maar wel hetzelfde als het vijf-honderdste déél.

Handige percentages en breuken

De volgende rijtjes percentages zijn handig om min of meer uit je hoofd te kennen. Veel rekenopgaven maken van deze rijtjes gebruik.

Handige breuken en percentages

Als je ooit een opgave krijgt als 62,5 % van 888, dan ziet dat er uit als een flinke rekenklus.
Als je dat helemaal wilt uitrekenen, dan krijg je:

1 % van 888 = 8,88.
62,5 % van 888 = 8,88 x 62,5. Dat gaat je uit het hoofd niet lukken, dus je gaat cijferend vermenigvuldigen.
Alles bij elkaar ben je een paar minuten zoek voor je bij de goede uitkomst bent.

Ken je de rijtjes met percentages en breuken dat je hier ziet staan, dan gaat het een heel stuk sneller:

62,5 % = 5/8 deel.
1/8 deel van 888 = 111
5/8 deel van 888 is dus 5 keer zoveel: 555.

Over korting

In de uitverkoop zie je vaak advertenties of winkelborden met spannende kortingen, vaak uitgedrukt in procenten. Soms is er een korting van 10, 20, 50%, soms zelfs nog hoger. Wat betekent dat voor het bedrag dat je bij kassa moet afrekenen? Laten we eens naar een voorbeeld kijken.

Je nieuwe broek wordt verkocht met 20 % korting. De originele prijs was € 100,- Wat betaal je? Je kunt dit uitrekenen door eerst 1 % van € 100 te nemen ( = € 1) en dat vermenigvuldigen met 20 ( = € 20). Je korting weet je nu, dus die haal je af van de originele prijs: €100 - € 20 = € 80 en dat is dan wat je afrekent.
Je kunt het ook anders uitrekenen: 20 % is het 1/5 deel. Je betaalt dus het 4/5 deel. Het 1/5 deel van € 100 is € 20 en dus is het 4/5 deel vier keer zo veel: € 80

Honderd procent

Als je naar de definitie van procent kijkt, dan heb je gezien dat één procent hetzelfde betekent als één van de honderd. Dat betekent ook, dat 100 % hetzelfde is als ‘alles’. Heb je 100 % van de appeltaart opgegeten, dan heb je dus de hele appeltaart op. Als iemand beweert dat hij 200 % van een appeltaart op heeft, dan is dat dus eigenlijk onzin, met 100 % is je appeltaart al verdwenen. Je hoort mensen wel eens zeggen dat ze voor 120% of 200 % hun best hebben gedaan om een bepaalde klus tot een goed einde te brengen. Je hoort ook wel eens andere percentages. Laten we helder zijn: méér dan honderd procent hun best doen, dat kan niet. Honderd procent is maximaal. Is zo’n uitspraak dan helemaal onzin? Rekenkundig misschien wel, maar men wil hiermee graag overdrijven om de optimale intentie aangeven, dat ze zich tot het uiterste zullen inspannen. Als je gewoon 100 % je best doen doe je het al geweldig, meer kan feitelijk niet.

Meer dan honderd procent

Toch kom je wel eens berichten tegen of statistieken, waar hogere percentages dan 100% worden gebruikt. Dit gaat altijd over vergelijkingen ten opzichte van bijvoorbeeld een vroegere situatie. De prijs van huizen is veel en veel hoger dan twintig jaar geleden, de waarde is vaak verdubbeld of verviervoudigd. Was de prijs van een huis destijds 100 %, dan kun je van een prijsstijging van meerdere honderden procenten spreken.

Lees verder

De tafeltjes oefenen, hoe doe je dat?