Wiskunde functieonderzoek
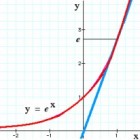 Functieonderzoek is een onderdeel van wiskunde dat beheerst moet worden in de bovenbouw. In dit artikel bekijken we achtereenvolgens nulpunten, de afgeleide, maxima en minima, buigpunten, en asymptoten. Uiteindelijk moet de grafiek van de functie getekend worden, hiervoor moet je eerst de eigenschappen van de functie onderzoeken. Voor moeilijke functies kun je altijd de GR (grafische rekenmachine) gebruiken. Aan de hand van voorbeelden wordt uitgelegd hoe het onderzoek in zijn werk gaat.
Functieonderzoek is een onderdeel van wiskunde dat beheerst moet worden in de bovenbouw. In dit artikel bekijken we achtereenvolgens nulpunten, de afgeleide, maxima en minima, buigpunten, en asymptoten. Uiteindelijk moet de grafiek van de functie getekend worden, hiervoor moet je eerst de eigenschappen van de functie onderzoeken. Voor moeilijke functies kun je altijd de GR (grafische rekenmachine) gebruiken. Aan de hand van voorbeelden wordt uitgelegd hoe het onderzoek in zijn werk gaat.
Functie's
Als voorbeeldfunctie's kiezen we de volgende functie's- f(x) = (x-4)² - 1
- g(x) = 3x^4 - 16x³ + 24x²
- h(x) = 10 / (x²-9)
- i(x) = 1/x
- j(x) = 3x² - x³
domein
Voor functieonderzoek is het van belang om het domein van een functie te onderzoeken. Het domein is het gebied waarop een bepaalde functie gedefinieerd is. Het kan voorkomen dat een functie voor zekere waarde van variabele x niet bestaat. Zo bestaat h(x) = 10 / (x²-9) niet voor x=3 en x=-3, omdat delen door nul niet is toegestaan. Men schrijft ook wel:- het domein van h(x) is R | {-3,3}
R is de verzameling van reële getallen.
nulpunten
Een functie snijdt de x-as in de zogenaamde nulpunten. Om deze punten te vinden moeten we de functie gelijk te stellen aan nul en de punten uit te rekenen.Stel f(x) = (x-4)² - 1.
Om de nulpunten te vinden stellen we : f(x) = (x-4)² - 1 = 0.
Oplossen levert x=3 of x=5. Deze waarden horen bij de nulpunten P (3,0) en Q (5,0).
stijgen en dalen
Om het verloop van een functie te begrijpen is het handig om te weten of een functie stijgt dan wel daalt. Hiervoor is het nodig dat we de afgeleide f ' (x) kennen.- f ' (x) = ((x-4)² - 1)' = (x² - 8x + 15)' = 2x - 8
- een andere schrijfwijze is f ' (x) = df(x)/dx, of d/dx f(x)
Voor x kleiner dan 4 is deze functie negatief, voor x = 4 gelijk aan nul, en voor x groter dan 4 positief.
Als de afgeleide f ' (x) negatief is zal de functie dalend zijn; voor f ' (x) positief stijgend.
Dit wordt als volgt aangegeven:
- ----------------------(x=4)+++++++++++
- ......... dalend......... Ι ......... stijgend.........
De min geeft aan dat de richtingscoëfficiënt (rico) negatief is, voor de plus is het positief. Het gebied van (x = -∞), min oneindig, tot (x=4) noemt men ook wel het interval <-∞,4>. Voor hetzelfde gebied, maar dan tot en met (x = 4), schrijft men <-∞,4].
maxima en minima
Maxima en minima worden ook wel extrema genoemd. Wanneer de afgeleide f ' (x) negatief is, is een functie dalend; voor een interval f ' (x) positief is een functie stijgend.Wat is er aan de hand bij f ' (x) = 0 ?
Wanneer de afgeleide = 0, dan is de functie niet stijgend of dalend; er is hier sprake van een maximum of minimum. De grafiek heeft (lokaal) een extreme waarde bereikt.
Wanneer de grafiek van dalend naar stijgend overgaat, is er sprake van een minimum; van stijgend naar dalend een maximum.
----------------------|+++++++++++ (x=minimum)
........dalend............stijgend.........
++++++++++++|---------------------- (x=maximum)
........stijgend..........dalend..........
Passen we deze regel toe op f(x) = (x-4)² - 1, dan vinden we f ' (x) = 2x-8 = 0. Oplossen levert x=4. Kleiner dan x=4 is de afgeleide negatief; groter dan x=4 positief. Er is hier sprake van het minimum M(4,-1).
- NB: wanneer een functie gedefinieerd is op een beperkt domein, dan leveren de grenzen van het domein lokale minima of maxima. Als een functie ophoudt in een randpunt, kan de functie daar niet verder dalen of stijgen.
buigpunten
Voor een buigpunt geldt dat de dubbele afgeleide f " (x)=0. Wanneer de afgeleide van een functie continu stijgend of dalend is maar tussendoor minder hard stijgt of daalt, dan kan er sprake zijn van een buigpunt. Het kenmerk van een buigpunt is dat de dubbele afgeleide f '' (x)=0.- Een buigpunt geeft aan dat de richtingscoëfficiënt een maximum of minimum bereikt heeft.
Stel g(x) = 3x^4 - 16x³ + 24x². Voor de afgeleide vinden we 12x³ - 48x² + 48x. Gelijkstellen aan nul levert 12x³ - 48x² + 48x=0, of 12x(x² - 4x + 4)=0. De oplossingen zijn x=0 of x=2. De dubbele afgeleide is gelijk aan 36x² - 96x + 48; deze functie is ook nul voor x=2, dit is dus een buigpunt. Het verloop van de afgeleide ziet er als volgt uit:
----------------------(x=0)+++++++++++(x=2)+++++++++++
........dalend....(minimum)..stijgend...(buigpunt)...stijgend.....
We vinden een minimum M(0,0) en een buigpunt B(2,16).
asymptoten
Een asymptoot is een lijn of kromme waarnaar een functie willekeurig dicht kan naderen als de variabele x een zekere waarde nadert. Een asymptoot kan een rechte lijn zijn. Stel h(x) = 10 / (x²-9). Delen door nul niet is toegestaan. Voor x=-3 en x=3 zal h(x) niet bestaan, maar heeft de functie een verticale asymptoot. Als deze waarden van x genaderd worden zal h(x) naar oneindig of min oneindig gaan, want delen door iets heel kleins levert iets heel groots.Wanneer x 'van boven' (hoger dan) 3 nadert zal (x²-9) positief zijn; 10 / (x²-9) nadert dan oneindig. Nadert x 'van onderen' (lager dan) 3 nadert dan is (x²-9) negatief; 10 / (x²-9) nadert dan min oneindig. In wiskundige taal:
- lim x↓3 h(x) = ∞
- lim x↑3 h(x) = -∞
 Bron: Tronic
Bron: Tronic- lim x→∞ h(x) = 0
- lim x→-∞ h(x) = 0
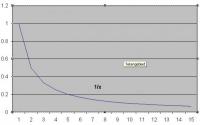
In de hiernaast getekende grafiek word geïllustreerd wat een asymptoot precies is. De functie i(x) = 1/x zal de waarde nul naderen als x naar oneindig gaat.
grafiek tekenen
Wanneer we een grafiek willen tekenen, lopen we bovengenoemde punten af. De functie wordt achtereenvolgens onderzocht op domein, nulpunten, de afgeleide (stijgen en dalen), extrema en buigpunten, en asymptoten. Er kan een tabel worden toegevoegd om inzichtelijk te maken waar de verschillende punten van de grafiek liggen.Stel j(x) = 3x² - x³.
- domein. De functie is gedefinieerd voor R, er zijn geen beperkingen of vreemde punten.
- nulpunten. Het oplossen van 3x² - x³ = 0 levert x=0 of x=3. Dus P(0,0) en R(3,0).
- afgeleide. j ' (x) = 6x - 3x². Gelijk stellen aan nul 6x - 3x² = 0 levert: x=0 0f x=2. Het tekenverloopschema van de afgeleide ziet er als volgt uit: ------------------(x=0)++++++++(x=2)------------------ Dit betekent een minimum bij P(0,0) en een maximum bij (2,4).
- buigpunten. De dubbele afgeleide j '' (x) = 6 - 6x. Gelijkstellen aan nul levert een buigpunt op voor x=1. Het tekenverloopschema van de dubbele afgeleide ziet er volgt uit: +++++++++(x=1)------------------ Het punt B(1,2) is een buigpunt; de grafiek zal op het interval [0,2] stijgen; tot x=1 stijgt ook de rico, daarna daalt de rico maar blijft positief tot x=2.
- asymptoten. Het domein van j(x) is R; er zijn geen waarden waarvoor j(x) niet gedefinieerd is. Er zal dan ook geen verticale asymptoot zijn. Er zijn ook geen horizontale asymptoten want de functie gaat naar oneindig voor x min oneindig, en als x naar oneindig gaat zal de functie naar min oneindig gaan.
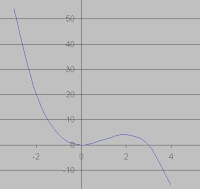
- tabel. Door een aantal punten in te vullen krijgen we een beeld van hoe j(x) ongeveer zal verlopen:
| x | -2 | -1 | 1 | 2 | 3 | 4 |
| j(x) | 20 | 4 | 2 | 4 | 0 | -16 |
 Bron: Tronic
Bron: TronicDit laatste kan ook op de GR (grafische rekenmachine), als de functies wat moeilijker worden.
succes!
© 2010 - 2025 Tronic, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
 Wiskunde - de afgeleide en extreme waardesHoe bereken je de extreme waardes, ook wel minimum en maximum, en hoe stel je een raaklijn op? Vaak wordt dit gezien als…
Wiskunde - de afgeleide en extreme waardesHoe bereken je de extreme waardes, ook wel minimum en maximum, en hoe stel je een raaklijn op? Vaak wordt dit gezien als…
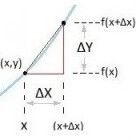 Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
 Het gebruik van het menu ‘CALC’ op de TI-84De rekenmachine genaamd TI-84 is een veelgebruikt hulpmiddel bij Wiskunde, Scheikunde, Economie- en Natuurkundelessen op…
Het gebruik van het menu ‘CALC’ op de TI-84De rekenmachine genaamd TI-84 is een veelgebruikt hulpmiddel bij Wiskunde, Scheikunde, Economie- en Natuurkundelessen op…
 Een toneelstuk maken: repetitiesOm een toneelstuk met succes te kunnen opvoeren moet er natuurlijk goed geoefend worden. In het theater noemen we dit re…
Een toneelstuk maken: repetitiesOm een toneelstuk met succes te kunnen opvoeren moet er natuurlijk goed geoefend worden. In het theater noemen we dit re…
Gerelateerde artikelen
Hoe bereken je machtsfuncties?Wat zijn machtfuncties? Machtfuncties zijn functies in de wiskunde die bekend worden geacht voor het centraal eindexamen…
Middelbare school uitkiezen - waarop moet men letten?Het is weer zover. De open dagen van de middelbare scholen komen er weer aan. Je zit in groep acht en je moet dit jaar e…
Bronnen en referenties
- Inleidingsfoto: Tronic
- Afbeelding bron 1: Tronic
- Afbeelding bron 2: Tronic
Tronic (33 artikelen)
Laatste update: 10-03-2017
Rubriek: Educatie en School
Subrubriek: Diversen
Bronnen en referenties: 3
Laatste update: 10-03-2017
Rubriek: Educatie en School
Subrubriek: Diversen
Bronnen en referenties: 3
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.