Slimme trucjes en tips die wiskunde makkelijker maken
 Wiskunde is niet echt ieders favoriete schoolvak. Logica lijkt niet altijd even logisch en ingewikkelde formules zorgen voor meer hoofdpijn dan een gemiddelde Chinese les. Er bestaan echter heel wat handige wiskundetrucjes om hoofdbrekers te voorkomen maar die op school jammer genoeg nooit worden aangeleerd.
Wiskunde is niet echt ieders favoriete schoolvak. Logica lijkt niet altijd even logisch en ingewikkelde formules zorgen voor meer hoofdpijn dan een gemiddelde Chinese les. Er bestaan echter heel wat handige wiskundetrucjes om hoofdbrekers te voorkomen maar die op school jammer genoeg nooit worden aangeleerd.- Percentages berekenen
- Vermenigvuldigen met 11
- Grote getallen vermenigvuldigen uit het hoofd
- Getallen vermenigvuldigen volgens de Japanse 'lijn'-methode
- Optellen en aftrekken van breuken
- De tafel van 9
- Vermenigvuldigingen van 6, 7, 8 en 9
- Het kwadraat van grote getallen berekenen
- Gebruik van de tekens 'groter dan' en 'kleiner dan'
- Weten of een getal deelbaar is door 3
- De kommagetallen van 'pi' onthouden
- Temperatuur in graden Celsius en Fahrenheit omrekenen
Wiskundige logica is niet altijd even duidelijk. Op school wordt er vaak verondersteld dat je bepaalde berekeningen en formules maar uit het hoofd moet leren. Er bestaan echter heel wat handige trucjes waarmee de meest ingewikkelde rekensommen een fluitje van een cent worden. Volgende tips leerde je vreemd genoeg nooit op school, maar zullen er vanaf nu voor zorgen dat wiskunde je favoriete vak wordt. Maak kennis met de wiskundeknobbel waarvan je niet eens wist dat je hem bezat.
Percentages berekenen
Wanneer je een percentage moet berekenen (bijvoorbeeld 60% van 500) laat dan het laatste nummer van het startcijfer vallen, en vermenigvuldig dit met het tiental van het percentage (50 x 6 = 300). Of ook wel: deel je startgetal door 100 (schuif de komma twee plaatsen naar links op) en vermenigvuldig met het percentagegetal.Een andere handige truc is te weten dat a% van b = b% van a (bijvoorbeeld 5% van 20 = 20% van 5)
Vermenigvuldigen met 11
Om 2-cijferige getallen makkelijk te vermenigvuldigen met 11, kan je dit trucje gebruiken: je splitst de 2 cijfers op en vult ertussen de som van beide cijfers in. Als deze som groter is dan 9, zet je de eenheid in het midden en tel je het tiental op bij het linker cijfer.Grote getallen vermenigvuldigen uit het hoofd
Een simpel trucje om twee getallen te vermenigvuldigen die beide tussen 90 en 100 gelegen zijn gaat als volgt: trek beide getallen af van 100. Dit geeft je resultaten a en b. 100- (a+b) geeft je de eerste twee cijfers van je eindresultaat. De laatste twee cijfers van je eindresultaat bekom je door a en b te vermenigvuldigen.Getallen vermenigvuldigen volgens de Japanse 'lijn'-methode
Een andere manier van vermenigvuldigen vinden we terug in Japan. De uitwerking van de 'lijnmethode' is gebaseerd op de Verdische wiskunde, die zijn oorsprong vindt in de Indiase overlevering. Het is niet altijd de snelste methode (voor getallen die bijvoorbeeld een 8 of 9 bevatten ben je wel even bezig met streepjes trekken), maar wel een leuke manier van rekenen. Het is onbegonnen werk om deze methode eenvoudig op papier uit te schrijven, maar wanneer dit visueel wordt voorgesteld in een video zal je zien dat je er snel zelf mee aan de slag kan.Optellen en aftrekken van breuken
Om sommen van breuken op te lossen maak je gebruik van de vlindermethode: De getallen onder de breuklijnen vermenigvuldig je, en en het eindresultaat boven de breuklijn is de som van de oorspronkelijke getallen, elk vermenigvuldigd met het getal dat ernaast onder de breuklijn staat. Dezelfde methode kan je gebruiken voor het aftrekken van breuken en voor de som van meerdere breuken.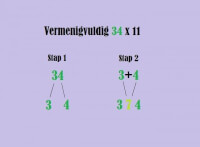 Vermenigvuldigen met 11 / Bron: Shary Heuninckx
Vermenigvuldigen met 11 / Bron: Shary Heuninckx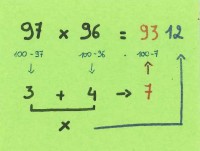 Grote getallen vermenigvuldigen uit het hoofd / Bron: Shary Heuninckx
Grote getallen vermenigvuldigen uit het hoofd / Bron: Shary Heuninckx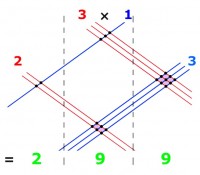 Getallen vermenigvuldigen volgens de Japanse 'lijn'-methode
Getallen vermenigvuldigen volgens de Japanse 'lijn'-methode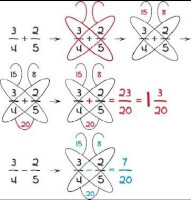 Optellen en aftrekken van breuken / Bron: Http://imgur.com/t/hacks/xnCqP
Optellen en aftrekken van breuken / Bron: Http://imgur.com/t/hacks/xnCqPDe tafel van 9
Gebruik je handen voor de tafel van 9: strek je 10 vingers uit. Bij 4 x 9 buig je je 4e vinder van links af gezien naar beneden. Het aantal gestrekte vingers links van je gebogen vinger (3) geeft de tientallen aan, het aantal gestrekte vingers rechts de eenheden (6). Het resultaat is in dit geval dus 36.Vermenigvuldigingen van 6, 7, 8 en 9
Gebruik je handen voor het vermenigvuldigen van 6, 7, 8 en 9. Ken volgende waarden toe aan je vingers: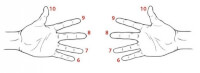 Waarden van de vingers / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPS
Waarden van de vingers / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPSNeem de volgende stappen:
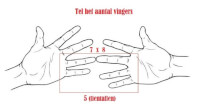 Stap 1 / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPS
Stap 1 / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPS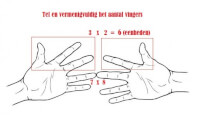 Stap 2 / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPS
Stap 2 / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPS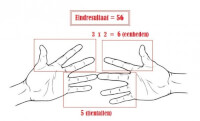 Stap 3 / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPS
Stap 3 / Bron: Http://www.instructables.com/id/Tables-of-6-7-8-and-9-in-your-hands/?ALLSTEPSHet kwadraat van grote getallen berekenen
Het kwadraat berekenen van getallen kleiner dan 100Trek het startgetal af van 100. Dit restgetal trek je af van het startgetal en je zet er twee nullen achter. Vervolgens bereken je het kwadraat van het restgetal. Tel daarna de twee berekende getallen op en je hebt je eindresultaat.
Voorbeeld
Het kwadraat van 89 berekenen: 89-11=78. Zet er 2 nullen achter: 7800. 11*11=121. 7800+121=7921
Het kwadraat berekenen van getallen groter dan 100
Volg dezelfde stappen als hierboven, maar tel het getal boven de 100 op bij het startgetal.
Voorbeeld
Het kwadraat van 104 berekenen: 104+4=108. Zet er 2 nullen achter: 10800. 4*4=16. 10800+16=10816
 Bron: Http://www.ducksters.com/kidsmath/inequalities.php
Bron: Http://www.ducksters.com/kidsmath/inequalities.phpGebruik van de tekens 'groter dan' en 'kleiner dan'
Op de volgende manier kun je onthouden aan welke zijde van het teken het grootste element moet komen te staan. Maak van je 'groter dan'/'kleiner dan' teken een gulzige krokodil, een happende PacMan of een vals gebit. Aangezien deze allemaal het liefst het grootste verorberen weet je dadelijk aan welke zijde van de vergelijking het grootste element moet komen te staan.Weten of een getal deelbaar is door 3
Wanneer de som van de cijfers waaruit het getal bestaat deelbaar is door 3, dan is het getal zelf ook deelbaar door 3.Voorbeeld
Het getal 2259. 2+2+5+9=18. 18 is deelbaar door 3, dus ook het getal 2259 is deelbaar door 3.
De kommagetallen van 'pi' onthouden
De kommagetallen van het cijfer 'pi' (3,141592653589793238462643383279...) komen overeen met het aantal letters van elk woord in onderstaande zinnetjes. Een handig ezelsbruggetje."Zie, 'k geef u thans, geleerden en leeken, ouden van dagen, frissche studenten, weinige regeltjes, die mij zijn gebleken, vaak nuttig te werken voor tal van docenten." (bron: Dr. Pieter Moree)
3,14159265358979323846264338
"Eva o lief, o zoete hartedief, uw blauwe oogen zyn wreed bedrogen." (een oud-Nederlands voorbeeld)
3,14159265358
"Wie u kent, o getal belangrijk en gepast, bezit ook grote waarheên, Ankervast."
3,141592653589
Kijk, 't moet u zeker verheugen te kunnen geven dit getal.
3,141592653
3,14159265358979323846264338
"Eva o lief, o zoete hartedief, uw blauwe oogen zyn wreed bedrogen." (een oud-Nederlands voorbeeld)
3,14159265358
"Wie u kent, o getal belangrijk en gepast, bezit ook grote waarheên, Ankervast."
3,141592653589
Kijk, 't moet u zeker verheugen te kunnen geven dit getal.
3,141592653
Temperatuur in graden Celsius en Fahrenheit omrekenen
Gebruik volgende formules om de omrekening te doen:- Van Celsius naar Fahrenheit: vermenigvuldig de temperatuur met 2 en tel er 30 bij. Bijvoorbeeld: 23°C = 76°F ((23x2) + 30)
- Van Fahrenheit naar Celsius: trek 30 af van de temperatuur en deel het resultaat door 2