Aard van een statistisch verband weergeven in een tabel
De aard of richting van een statistisch verband kunnen we weergeven door middel van een kruistabel of een gemiddelde tabel. Een kruistabel wordt gebruikt om het verband tussen categorale (nominale en ordinale) variabelen te weergeven. Een gemiddelde tabel wordt gehanteerd om het verband tussen een afhankelijke variabele op intervalniveau te weergeven en een onafhankelijke variabele die ofwel op ordinaal, nominaal of intervalniveau gemeten is. Voor het overzicht is het belangrijk dat de afhankelijke variabele de rijen dient te weerspiegelen en de onafhankelijke variabele de kolommen.Aard van een statistisch verband
Zoals vermeld in het artikel over bivariate en multivariate analyse, dienen we om een statistisch verband te onderzoeken tussen variabelen ons 4 dingen af te vragen. Wanneer we bij stap 4 zijn aangekomen (wat is de aard of richting van het verband), komt het erop neer om het verband dat we hebben gevonden te specificeren.Kruistabel of tabel met gemiddelden
In de statistiek kunnen we dergelijk verband (opnieuw afhankelijk van het meetniveau van de variabele), door middel van 2 manieren weergeven:- via kruistabellen
- via tabellen met gemiddelden
De afhankelijke variabele dient in de rijen te verschijnen, terwijl de onafhankelijke variabele boven de kolommen moet staan.
Kruistabellen
Verband categorale variabelenKruistabellen dienen om het verband tussen categorale variabelen te weergeven. Dit wil dus zeggen: variabelen die gemeten zijn op nominaal of ordinaal niveau.
Voorbeeld
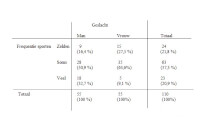
Zo kunnen we ook nog de andere verbanden per categorie observeren en over welke totalen het gaat. Er wordt via percentages gewerkt omdat deze de juiste verhouding weergeven naargelang de grootte van de steekproef. In dit geval is het niet zo'n probleem als we in aantallen spreken om het verschil tussen mannen en vrouwen duidelijk te maken. Als we zeggen dat er bv. 9 mannen maar zelden sporten, terwijl dit er bij de vrouwen 15 zijn, is dit ook wel duidelijk gezien we voor beide groepen met 55 proefpersonen werken. Wanneer we in een aselecte steekproef bv. maar 60 mannen hebben en 40 vrouwen en 8 mannen zeggen dat ze zelden sporten, terwijl dit er bij de vrouwen ook 8 zijn, kunnen we niet besluiten dat er evenveel mannen en vrouwen zelden sporten, omdat onze verhouding anders is: 8/60 tegen 8/40.
