Hypergeometrische verdeling: trekkingen zonder teruglegging

De hypergeometrische verdeling is een discrete kansverdeling, waarbij men bij aselecte trekkingen uit de populatie N, met M successen, de kans op m successen gaat berekenen via een steekproef n. Belangrijk hierbij is dat de trekkingen zonder teruglegging gebeuren. Om de kans op successen m: p(m) te berekenen doet men beroep op een specifieke formule. De hypergeometrische verdeling verschilt in belangrijke mate van de binomiale verdeling. Een belangrijk eigenschap is dat men bij de hypergeometrische verdeling met aselecte trekkingen zonder teruglegging werkt, terwijl dit bij de binomiale verdeling niet is.

De hypergeometrische verdeling

Voorbeeld

Stel dat men in een vaas 5 rode, 4 gele en 3 groene knikkers heeft gelegd. Men neemt achtereenvolgens (dus knikker per knikker) 3 knikkers uit de vaas. Hoe groot is dan de kans dat je precies 2 groene eruit neemt.

Uitwerking via formule hypergeometrische verdeling

We zien hierbij dat de N=12 (5+4+3) en n= 3 (de steekproef van 3 knikkers uit de vaas te nemen). Belangrijk hierbij is dat men de kans zal berekenen zonder teruglegging van de knikkers. Er ontstaat dus telkens een nieuwe kans op succes/mislukking. Als men bijvoorbeeld vanaf de eerste beurt een groene knikker eruit neemt, zal de kans op een nieuwe groene knikker verminderen naar 2 op 11. Dit in tegenstelling tot bij de binomiale verdeling, waarbij men wel met teruglegging werkt. De mate waarin men dus wel of niet met teruglegging werkt heeft dus een serieuze invloed op de kans op succes. Om de totale kans op dit succes te berekenen werkt men via volgende formule.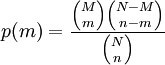

Teller

Hierbij staat p(m) dus voor de kans op succes. De hoofdletter M verwijst hier naar het totaal van de 'groene groep knikkers'. In dit geval zijn we geïnteresseerd om 2 groene knikkers (van de 3) in de vaas te nemen. Hier is dus M gelijk aan 3. Het aantal groene knikkers dat we dus verplicht moeten grijpen op die 3 beurten is 2. We zien dus dat kleine m gelijk is aan 2. De eerste term tussen haakjes is dus gelijk aan 3 op 2. Daarnaast dienen we de rest van de overblijvende knikkers in de vaas te vermelden. We hebben nog 9 knikkers over. Van die 9 knikkers mogen we nog 1 knikker 'misgrijpen', omdat ons experiment peilt naar het trekken van 2 groene knikkers en er dus 1 uit de andere groepen mag komen. We weergeven deze totale term door N-M op n-m. Als we deze waarden invullen wordt dit voor N-M:12-3 en voor n-m: 3-2. Samengevoegd wordt dit dus 9 op 1.

Noemer

Onder de breukstreep vermelden we het aantal knikkers, met daaronder het aantal knikkers dat we zullen trekken: 12 op 3 dus. Deze bewerking kunnen we vlot uitrekenen via ons grafisch rekenmachine met de formule: (3ncr2 * 9ncr1) / 12ncr3 = 0,1227. Dit wil dus zeggen dat we een kans hebben van 12,27 procent om uit de groep van 12 knikkers, met daarin 3 groene en 9 andere, op 3 beurten toch 2 groene knikkers te grijpen. Een lage kans dus, wat logisch is gezien het klein aantal groene knikkers in de vaas en we er toch 2 moeten nemen van die 3 in 3 beurten. Wanneer men bijvoorbeeld gevraagd had om op 4 beurten 2 rode knikkers eruit te halen, zou de formule er als volgt uitzien:
(5ncr2 * 7nrc2) / 12ncr4 = 0,4242.

Controle uitwerking

Merk op dat de totalen in de noemer en teller moeten overeenkomen. In het eerste voorbeeld moet M+ (N-M) gelijk zijn aan N in de noemer en m+(n-m) moet gelijk zijn aan m in de noemer. Uitgedrukt voor het eerste voorbeeld is dit: 3+ (12-3) = 12 en 2+ (3-2) = 3. We zien dus hier dat dit overeenkomt met de noemer (12 op 3). Het is belangrijk om dit altijd na te kijken ter controle.