Binomiale verdeling

De binomiale verdeling is de verdeling van de kans op een aantal successen (k), berekend aan de hand van onafhankelijke experimenten (n), gegeven een zekere kans hierop (p). De binomiale verdeling kan zowel (in gemakkelijke gevallen) handmatig, via de formule, als via een grafisch rekenmachine worden berekend. Hiernaast bestaat er ook een binomiale tabel, waar de kans op k aantal successen reeds is berekend. Het kan zowel een enkelvoudige als een cumulatieve tabel (waar de kansen opgeteld worden) zijn.

Kenmerken van de binomiale verdeling

Men mag de binomiale verdeling niet zomaar gebruiken bij de kansberekening. Er moet aan volgende kenmerken voldaan zijn:

• Onafhankelijke kansexperimenten (ook wel 'kans met teruglegging' genoemd)
• Constante kans op succes
• Vast aantal experimenten
• 2 antwoordmogelijkheden (succes/mislukking)

Voorbeeld: Wat is de kans dat een student 2 van de 4 vierkeuzevragen correct beantwoordt als hij gokt.

Handmatige uitwerking van de kans

De kans om het juiste antwoord (J) te gokken bij een vierkeuzevraag is 1/4. Echter het volstaat niet om de kansen met elkaar te vermenigvuldigen: 1/4 (J) * 1/4 (J) * 3/4 (F) * 3/4 (F), want dan gaan we er verkeerdelijk vanuit dat dit de enige combinatie is waarin men 2 juiste en 2 foute antwoorden zal geven. In dit geval zou de kans 0,0352 bedragen (3,52 procent). Hier houden we dus geen rekening met het aantal mogelijke combinaties waarmee we 2 juiste en 2 foute antwoorden kunnen geven. Deze zullen een invloed hebben op de grootte van de kans. Er zijn namelijk 6 combinaties:

• JJFF (zoals hierboven in het voorbeeld vernoemd)
• JFJF
• FJFJ
• JFFJ
• FFJJ
• FJJF

Om dus de volledig juiste kans te kunnen geven moeten we onze kans (0,0352) nogmaals vermenigvuldigen met 6 (= aantal mogelijke combinaties). Dit maakt dat we onze kans hier verhogen. 6*0,0352 is namelijk 0,2109, ofwel 21,09 procent. Het antwoord op dit vraagstuk luidt dus: de kans dat een student 2 van de 4 vierkeuzevragen correct beantwoordt is 21,09 procent.

Berekening door middel van binomiale formule

We kunnen dit vraagstuk ook oplossen door middel van volgende formule: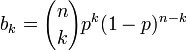

Binomiaalcoëfficient

Waarbij het belangrijk is om eerst te weten hoe we de binomiaalcoëfficiënt uitrekenen: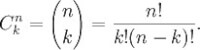


Hierbij staat n dus voor het aantal experimenten (= 4 meerkeuzevragen) en k voor het aantal successen dat we willen hebben. Dit is hier 2. We vullen dus bij n en k respectievelijk 4 en 2 in. Het uitroepteken staat voor 'faculteit' en deze optie bevindt zich in grafische rekenmachines, wat het handiger maakt bij grotere getallen om deze coëfficiënt uit te rekenen. Als we dit verder handmatig uitrekenen is dit gelijk aan 4.3 / 2.1 = 6. Hier zien we dat we door middel van deze coëfficiënt het aantal mogelijke combinaties hebben weergegeven (=6). Om nu de kans 'op succes' te berekenen dienen we terug te gaan naar de eerste formule.


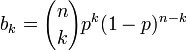
We hebben hier reeds gezien dat de eerste term (de binomiaalcoëfficiënt) gelijk is aan 6. Nu kunnen we dus de andere termen invullen. We vullen voor p 0,25 in. Dit is immers de kans dat we een juist antwoord geven. We doen dit tot 'de k-de' macht. Zoals eerder gezien is de 'k' de aanwijzing voor het aantal successen in ons experiment (=2). We moeten nu ook vermenigvuldigen met de kans op 'geen succes' tot de 'n-k'de macht. In feite is dit juist het omgekeerde van de term die we zojuist besproken hebben. Als de kans op succes gelijk is aan 0,25, dan is de kans op mislukking gelijk aan 0,75. De som van de kansen moet immers altijd gelijk zijn aan 1. Vandaar dat er dus ook 1-p wordt gebruikt in de formule (1-0,25= 0,75). Net zoals we nu de tegengestelde kans berekend hebben doen we dit ook met de tegenhanger van de k-de macht. Ons aantal experimenten (n) is gelijk aan 4. Nu moeten we nog n-k bepalen. We kijken dus naar onze n en k. Deze zijn 4 en 2. Hieruit zien we dus dat we 0,75 tot de tweede macht (n-k) moeten verheffen. Als we dit uitrekenen bekomen we dus 6* 0,625 * 0,5625 = 0,2109. Merk op dat 0,625 * 0,5625 = 0,0352.

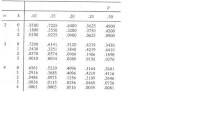Binomiale tabel

Om het ons gemakkelijker te maken zijn er ook binomiale tabellen aanwezig, die deze kansen voor ons reeds hebben uitgerekend. We kunnen inzake deze tabellen nog een onderscheid maken tussen een enkelvoudige en een cumulatieve binomiaaltabel.

We vinden hier ook de kans 0,2109 terug die we zonet hebben berekend. In de plaats van deze waarde zal bij een cumulatieve tabel de waarde 0,9492 staan, met daarboven 0,7383 (waar in bovenstaande tabel het getal 0,4219 staat). Om dan de individuele kans voor k=2 te berekenen uit deze cumulatieve tabel dienen we 0,9492-07383 te doen. Dit is immers gelijk aan 0,2109. De cumulatieve tabel is dus niets anders dan de optelling van de individuele kansen. Daar waar het getal 0,4219 staat zal bij de cumulatieve reeds 0,7383 staan. Dit komt dus omdat de individuele opgetelde kansen bij 1 en 2 in de enkelvoudige tabel (0,3164+0,4219), gelijk zijn aan 0,7383 enz...