Differentiëren met de TI grafische rekenmachines
 De grafische rekenmachines van Texas Instruments worden anno 2014 veel gebruikt in het voortgezet en hoger onderwijs, bijvoorbeeld de TI-83, TI-84 of de TI-Nspire. Veel gebruikers kennen echter de geavanceerde functies van hun grafische rekenmachines niet. Daarbij hebben ook veel scholieren moeite met het bepalen van de helling van functies, bijvoorbeeld door te differentiëren. Hier worden twee mogelijkheden voor bepalen van de helling van functies op de TI-rekenmachines besproken: de numerieke methode en de algebraïsche methode (ook wel eens de symbolisch genoemd).
De grafische rekenmachines van Texas Instruments worden anno 2014 veel gebruikt in het voortgezet en hoger onderwijs, bijvoorbeeld de TI-83, TI-84 of de TI-Nspire. Veel gebruikers kennen echter de geavanceerde functies van hun grafische rekenmachines niet. Daarbij hebben ook veel scholieren moeite met het bepalen van de helling van functies, bijvoorbeeld door te differentiëren. Hier worden twee mogelijkheden voor bepalen van de helling van functies op de TI-rekenmachines besproken: de numerieke methode en de algebraïsche methode (ook wel eens de symbolisch genoemd).
Numerieke methode
Het bepalen van de helling van een grafiek op een bepaalde plek kan gemakkelijk door de nDeriv-functie. Deze functie kan je vinden door op MATH te drukken en de achtste optie in het tabblad MATH te selecteren. De nDeriv-functie wordt aangeroepen door nDeriv(functievoorschrift, variabele, x-waarde). Bij functievoorschrift moet de vergelijking worden ingevuld waarvan je de helling wilt bepalen (bijvoorbeeld x^2+6x). Bij variabele moet de variabele waarin de functie is gegeven worden ingevuld (normaliter X). Bij de x-waarde moet de waarde worden ingevuld waar de helling van de functie bepaald moet worden.De nDeriv-functie kan ook in het grafiekenscherm worden gebruikt. Als je bijvoorbeeld de functie op Y1 gegeven is, kan bij Y2 de regel nDeriv(Y1,X,X) worden ingevuld, zodat op elk punt de helling van de Y1-functie gegeven wordt.
Bij deze numerieke methode weet men echter nog niet wat het functievoorschrift van de helling. Daarvoor is de algebraïsche methode, die erg onbekend is bij de gebruikers.
Algebraïsche methode
In tegenstelling tot wat veel gebruikers denken, zijn de basis TI-rekenmachines ook in staat om algebraïsch te differentiëren: bijvoorbeeld om van y= x^2 + 6x naar y’ = 2x + 6 te gaan. Er bestaan programma’s die alleen werken voor bepaalde simpele formules zoals polynomen, maar deze programma’s zijn niet echt flexibel en voegen vrij weinig toe. Een programma dat wel alle soorten formules kan differentiëren is Symbolic.Het installeren van Symbolic is simpel door Symbolic te downloaden van de website en te uploaden naar je rekenmachine met het bijgeleverde kabeltje. Vervolgens is Symbolic verschenen in de lijst met Apps. Als je Symbolic opent in het Apps menu, kan er vervolgens worden gekozen om Symbolic te installeren. Als Symbolic is geïnstalleerd, kunnen de functies van Symbolic worden benaderd door twee keer op de MATH-toets te drukken. Er wordt dan een nieuw menu geopend, waarbij de d(-functie in het tweede tabblad voor dit doeleinde het interessantst is.
De functie d( wordt gegeven door d(“functievoorschrift”,”variabele”). Let hierbij op de aanhalingstekens die verplicht zijn. Het voorbeeld van hierboven zou dand(“X^2+6*X”,”X”) worden, waarbij het goede antwoord “2*X + 6” weergegeven wordt. Een moeilijker voorbeeld is d(“X^2-ln(X)”,”X”), dat als antwoord “2*X – 1/X” geeft. Als de uitvoer van het Symbolic-programma te onduidelijk is, kan ook de applicatie PrettyPrint worden gebruikt. Met deze applicatie kunnen de vergelijkingen die Symbolic als uitvoer geeft mooi worden weergeven in het grafische scherm.
© 2014 - 2025 Schulti, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
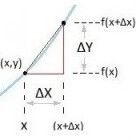 Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
 Wiskunde - logaritmen, het getal e, lnWil je graag weten wat een logaritme, het getal e, en een ln is? Deze wiskundige termen zien er erg ingewikkeld uit. Wan…
Wiskunde - logaritmen, het getal e, lnWil je graag weten wat een logaritme, het getal e, en een ln is? Deze wiskundige termen zien er erg ingewikkeld uit. Wan…
 Hoeken berekenen met de tangens functieOp de middelbare school krijgt bijna elke leerling te maken met het berekenen van hoeken. De ene leerling krijgt dit op…
Hoeken berekenen met de tangens functieOp de middelbare school krijgt bijna elke leerling te maken met het berekenen van hoeken. De ene leerling krijgt dit op…
 Rekenmachines: drie modellen voor verschillend gebruikOm iets uit te rekenen wat niet een-twee-drie uit het hoofd kan gebeuren wordt al snel naar een rekenmachine gegrepen. I…
Rekenmachines: drie modellen voor verschillend gebruikOm iets uit te rekenen wat niet een-twee-drie uit het hoofd kan gebeuren wordt al snel naar een rekenmachine gegrepen. I…
 Voorbereiden en datum Citotoets 2019 (Cito Eindtoets 2019)Ook in het schooljaar 2018/2019 is weer een flink deel van de leerlingen van groep 8 bezig met voorbereiden op de Citoto…
Voorbereiden en datum Citotoets 2019 (Cito Eindtoets 2019)Ook in het schooljaar 2018/2019 is weer een flink deel van de leerlingen van groep 8 bezig met voorbereiden op de Citoto…
 Sintquiz over liedjes voor kinderen en dementerendenHet Sinterklaasfeest is van origine vooral een decemberfeest voor de kinderen. Met ouderen met dementie door bijvoorbeel…
Sintquiz over liedjes voor kinderen en dementerendenHet Sinterklaasfeest is van origine vooral een decemberfeest voor de kinderen. Met ouderen met dementie door bijvoorbeel…
Gerelateerde artikelen
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.