Vermoedens en Bewijzen - Wiskunde
 Bij het vak wiskunde op het VWO, en dan met name Wiskunde B, is het onderdeel vermoedens en bewijzen belangrijke stof voor het eindexamen. Bij dit onderdeel moet je met behulp van regels en stellingen hoeken en zijden gaan bewijzen. In dit artikel wordt uitgelegd hoe je de meest voorkomende regels en stellingen kunt toepassen op de figuren.
Bij het vak wiskunde op het VWO, en dan met name Wiskunde B, is het onderdeel vermoedens en bewijzen belangrijke stof voor het eindexamen. Bij dit onderdeel moet je met behulp van regels en stellingen hoeken en zijden gaan bewijzen. In dit artikel wordt uitgelegd hoe je de meest voorkomende regels en stellingen kunt toepassen op de figuren.Hoeken en lijnen
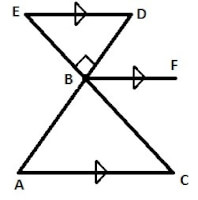 Figuur 1: hoeken
Figuur 1: hoeken- Overstaande hoeken: de overstaande hoeken bij twee kruisende lijnen zijn even groot. Hoek ABC = hoek DBE (overstaande hoeken).
- F- en Z-hoeken: wanneer twee lijnen evenwijdig aan elkaar lopen, te herkennen aan bijvoorbeeld de pijltjes door de lijnen, kan je bewijzen dat hoek CAB = hoek BDE (Z-hoeken) en hoek CBF = hoek BED (F-hoeken).
- Gestrekte hoek: dit is een hoek van 180 graden, oftewel een rechte lijn. In dit geval is hoek ABE + hoek DBE = 180 graden (gestrekte hoek).
- Rechte hoek: dit is een hoek van 90 graden. Een rechte hoek is te herkennen aan een soort vierkante in de hoek, zoals in de figuur te zien is bij hoek EBD.
Lijnen
- Middelloodlijn: een middelloodlijn deelt een lijn doormidden en geeft hoeken van 90 graden. De middelloodlijn door S en F verdeelt AB in twee gelijke stukken.
- Bissectrice: de bissectrice verdeelt een hoek in twee gelijke hoeken. Zo verdeelt de bissectrice van hoek B (de lijn BK) de hoek B in de twee gelijke hoeken hoek CBK en hoek ABK (bissectrice).
- Hoogtelijn: de hoogtelijn is een lijn vanuit een hoek loodrecht op de overstaande zijde. In het figuur is CE de hoogtelijn vanuit hoek C, die loodrecht op AB staat.
- Zwaartelijn: de zwaartelijn is de lijn die vanuit een hoek naar de overstaande zijde loop, waardoor die overstaande zijden in twee gelijke stukken verdeeld wordt. In het figuur in de lijn AD de zwaartelijn vanuit hoek A, zodat CD = BD (zwaartelijn).
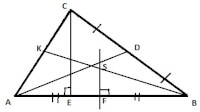 Figuur 2: lijnen
Figuur 2: lijnenDriehoeken
Congruente en gelijkvormige driehoekenCongruent: twee driehoeken zijn congruent (gelijk), wanneer ze aan één van onderstaande voorwaarden voldoen.
- HZH: een zijde en twee aanliggende hoeken gelijk hebben
- ZHH: een zijde, een aanliggende hoek en de tegenoverliggende hoek gelijk hebben
- ZHZ: twee zijden en de ingesloten hoek gelijk hebben
- ZZZ: alle zijden gelijk hebben
- ZZR: twee zijden en de rechte hoek tegenover één van die zijden gelijk hebben
Gelijkvormig: twee driehoeken zijn gelijkvormig, wanneer ze aan één van onderstaande voorwaarden voldoen.
- hh: twee hoeken gelijk hebben
- zhz: een hoek en de verhouding van de aanliggende zijden gelijk hebben
- zzz: de verhoudingen van alle zijden gelijk hebben
- zzr: een rechte hoek en de verhouding van twee niet-aanliggende zijden gelijk hebben
Driehoeken
- Hoekensom: dit is de som van alle drie de hoeken, die samen altijd 180 graden zijn.
- Gelijkbenig: een gelijkbenige driehoek is een driehoek met twee gelijke zijden. De hoeken in een gelijkbenige driehoek zijn even groot. Hoek ABC = hoek ACB (gelijkbenige driehoek).
- Gelijkzijdig: een gelijkzijdige driehoek is een driehoek, waarvan alle drie de zijden even lang zijn. Ook zijn alle hoeken even groot Volgens de hoekensom is elke hoek dan 60 graden.
- Rechthoekig: een rechthoekige driehoek is een driehoek, waarvan één van de drie hoeken een rechte hoek is (90 graden).
- Geodriehoek: een geodriehoek is een driehoek, waarvan één hoek een rechte hoek is en de andere twee hoeken gelijk zijn en dus beide 45 graden. Dit wordt ook wel een gelijkbenige rechthoekige driehoek genoemd.
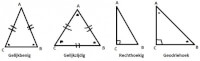 Figuur 3: driehoeken
Figuur 3: driehoekenVierhoeken
- Hoekensom: de hoekensom van een vierhoek is de som van alle vier de hoeken, die samen altijd 360 graden moeten zijn.
- Parallellogram: een parallellogram is een vierhoek met twee paar evenwijdige zijden, waarvan de overstaande zijden even lang zijn. In een parallellogram zijn ook de overstaande hoeken even groot. De diagonalen van een parallellogram delen elkaar middendoor
- Ruit: een ruit is een vierhoek met vier even lange zijden. De diagonalen van een ruit delen de hoeken middendoor en snijden elkaar loodrecht.
- Rechthoek: een rechthoek is een vierhoek met vier rechte hoeken. De diagonalen van een rechthoek zijn even lang.
- Vierkant: een vierkant is een vierhoek met vier even lange zijden en vier rechte hoeken.
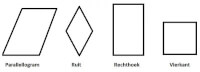 Figuur 4: vierhoeken
Figuur 4: vierhoekenCirkels
Koorde en raaklijnIn een cirkel behoren gelijke bogen bij gelijke koorden. De hoek tussen een raaklijn aan de cirkel en een koorde van die cirkel, waarvan een eindpunt het raakpunt is, is even groot als de bij die koorde behorende omtrekshoek. Ook staat een raaklijn aan een cirkel loodrecht op de verbindingslijn van het middelpunt van de cirkel en het raakpunt.
- Middelpuntshoek: een middelpuntshoek van een cirkel is een hoek, waarvan het hoekpunt het middelpunt van de cirkel is.
- Omtrekshoek: een omtrekshoek van een cirkel is een hoek, waarvan het hoekpunt op de cirkel ligt en de benen de cirkel snijden. Een omtrekshoek is gelijk aan de helft van de middelpuntshoek, die dezelfde koorde insluit als die omtrekshoek.
- Constante hoek: als punt D aan dezelfde kant van AB ligt als punt C en de hoeken ADB en ACB zijn even groot, dan liggen C en D op dezelfde cirkelboog AB. Als punt C over een cirkelboog AB tussen de punten A en B beweegt, dan verandert de grootte van de omtrekshoek ACB niet.
- Thales: als driehoek ABC rechthoekig is in hoek C, dan ligt punt C op een cirkel, waarvan de lijn AB de middellijn is van die cirkel.
- Koordenvierhoek: van een koordenvierhoek liggen alle vier de hoekpunten op een cirkel. De overstaande hoeken zijn samen 180 graden.
Achter een regel, die je net bewezen hebt, zet je altijd tussen haakjes de regel of stelling die je gebruikt hebt. Voorbeeld: hoek A + hoek B = 180 graden (gestrekte hoek) of in een driehoek hoek A + hoek B + hoek C = 180 graden (hoekensom driehoek).