Percentielscores: uitleg en interpretatie

Steeds vaker zijn percentielscores te zien bij de resultaten van toetsen en testen. Percentielen worden vaak onterecht vergeleken met procenten. Hoewel ze veel met elkaar gemeen hebben, zijn de termen niet volledig uitwisselbaar. Percentielscores werken volgens de normaalverdeling, waardoor er aan de hand van deze scores gemakkelijk gezegd kan worden of dit een goede of slechte score is.

De achtergrond van de percentielscores

Wanneer je een toets hebt gemaakt en hier in totaal 75 punten voor hebt gehaald, weet je nog niet goed of je juist blij moet zijn of teleurgesteld. Pas wanneer je weet hoe anderen dezelfde toets hebben gemaakt, en je jezelf ergens mee kunt vergelijken, heeft het aantal punten dat je hebt behaald een betekenis. Stel je voor dat 90% van de mensen die dezelfde toets hebben gemaakt, lager scoren dan 75 punten. Jouw percentielscore op de toets is dan 90.

De normaalverdeling

In de statistiek gaat men er vanuit dat alles verdeeld is volgens de normale verdeling. Grofweg betekent dit dat bij een testscore de meeste mensen rond het gemiddelde scoren en er slechts een paar uitschieters zijn met een zeer hoge, of zeer lage score. Om dit nog wat beter uit te leggen, is een ander voorbeeld duidelijker:

Verdeling

Voorbeeld
Stel je voor, je sorteert alle mensen uit je stad of dorp op lengte naast elkaar, mensen die precies even lang zijn, gaan achter elkaar staan. De kleinste mensen staan helemaal links en de langste mensen staan helemaal rechts. Als je van de voorkant naar je verdeling kijkt, zul je niet zoveel bijzonders zien, de mensen worden steeds groter. Stel je nu eens voor dat je van bovenaf naar deze mensen kijken. Dan zul je waarschijnlijk zien dat er in het midden veel mensen achter elkaar staan met dezelfde lengte. Naarmate je verder naar links of naar rechts kijkt, zul je steeds minder mensen achter elkaar zien staan. De verdeling ziet er van bovenaf grofweg uit als op de afbeelding.

De verdeling van de mensen, zoals in het voorbeeld van bovenaf gezien, noem je de normaalverdeling. In een normaalverdeling zullen de meeste mensen rond het gemiddelde zitten, bij een toets behalen de meeste mensen dus een score rond het gemiddelde. Naarmate je verder naar boven of naar beneden kijkt, zullen er minder mensen voorkomen.

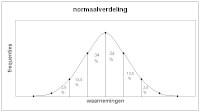Voorbeeld van normaalverdeling

Percentielscores en de normaalverdeling

In het voorbeeld zie je hoe de mensen verdeeld zijn over de normaalverdeling. Helemaal onderin, in het onderste stukje (2 standaardafwijkingen onder het gemiddelde) zit ongeveer 2,5% van de gehele populatie. Als je naar de hoogste scores kijkt, 2 standaarddeviaties boven het gemiddelde, zie je ook weer 2,5% van de populatie zitten. Wanneer je iets dichter bij het gemiddelde gaat kijken, zie je 1 standaarddeviatie onder en 1 standaarddeviatie boven het gemiddelde, 13,5% van de bevolking. De rest, grofweg 68%, zit verspreid rond het gemiddelde.

Hier komen we gelijk bij de percentielscores. Zoals genoemd zegt een percentielscore dus iets over het percentage van de bevolking dat lager of gelijk scoort aan de score die jij behaald hebt. Heb je een percentielscore van 1 of 2, dan heb je dus een uitzonderlijk lage score en zit jouw score in het laagste stukje van de normaalverdeling. Heb je een percentielscore van 23, dan betekent dit alweer dat jouw score in het gemiddelde gebied ligt.

Naamgeving van de percentielscores

In onderstaande tabel kun je de naamgeving van de scores aflezen. Wanneer is het nog gemiddeld? Wanneer zit je boven of onder het gemiddelde?

Percentielscore	Naamgeving
0 - 3	Zeer laag
3 - 10	Laag
10 - 16	Beneden gemiddeld
16 - 84	Gemiddeld
84 - 90	Boven gemiddeld
90 - 98	Hoog
98 - 100	Zeer hoog

Vergelijking van percentielscores met andere scores

Omdat de percentielscores normaal verdeeld zijn, zijn ze gemakkelijk te vergelijken met andere, veelgebruikte, scores. Ze zijn bijvoorbeeld gemakkelijk te vergelijken met C-scores.

Vergelijking met C-scores:

C-score	Percentielscore
0	0 - 3
1	4 - 8
2	9 - 14
3	15 - 23
4	24 - 40
5	40 - 60
6	61 - 75
7	76 - 90
8	91 - 97
9	97 - 100