Uitleg productregel
 De productregel is een regel voor het differentiëren van een formule waarin twee termen worden vermenigvuldigd. Met deze regel kan men dus de afgeleide van een formule berekenen. In dit artikel lees staat hoe de productregel gebruikt moet worden en daarmee dus ook hoe de afgeleide berekend moet worden.
De productregel is een regel voor het differentiëren van een formule waarin twee termen worden vermenigvuldigd. Met deze regel kan men dus de afgeleide van een formule berekenen. In dit artikel lees staat hoe de productregel gebruikt moet worden en daarmee dus ook hoe de afgeleide berekend moet worden.
Wanneer gebruikt men de productregel in de wiskunde?
De productregel gebruikt men om formules waarin twee of meer termen vermenigvuldigd worden met elkaar te differentiëren. Daarvan komt dus ook de naam 'productregel', want het gaat om het product van een formule. Een voorbeeld formule waarbij de productregel wordt gebruikt: F(x)= 3x 5x³De standaard regel van de productregel
Wanneer men de productregel wil toepassen gebruikt men altijd de volgende standaard regel:F'(x) = f'(x) g(x) + f(x) g'(x)
Stappenplan voor het gebruiken van de productregel:
- f(x) en g(x) staan voor een bepaalde term in de formule die gedifferentieerd moet worden. Men wijst de twee termen die in de originele formule met elkaar vermenigvuldigd worden beide toe aan f(x) of g(x).
- Daarna gaat men de termen invullen in de productregel. Eerst vult men dus de afgeleide van de term die aan f(x) is toegewezen in. Dan vult men de term die aan g(x) is toegewezen in. Vervolgens vult men de term die aan f(x) is toegewezen in.
- Tot slot wordt de afgeleide van de term die aan g(x) is toegewezen in gevuld.
- Indien mogelijk wordt de afgeleide nog kortere geschreven.
In principe is de afgeleide dan al berekend. Het zal waarschijnlijk nog moeilijk te begrijpen zijn, daarom volgt hieronder een voorbeeld som met uitleg.
Een voorbeeld van het gebruik van de productregel met uitleg:
Om de productregel goed uit te kunnen leggen gebruiken we een voorbeeld formule. We nemen als wiskundige voorbeeld formule F(x)= 3x 5x³. In deze formule worden twee termen met elkaar vermenigvuldigd. De eerste term is 3x. De tweede term is 5x³. Daardoor weten we dat we de productregel moeten gebruiken. Anders zouden we de kettingregel, quotientregel of somregel moeten gebruiken.Termen toewijzen en de productregel toepassen
Om de standaard regel (F'(x) = f'(x) g(x) + f(x) g'(x)) toe te passen onze formule (F(x)= 3x 5x³) moeten we de twee termen 3x en 5x³ toewijzen aan de letters f en g uit de standaard regel. 3x wijzen we toe aan de letter f en 5x³ wijzen we toe aan de letter g. Deze toewijzing had net zo goed andersom kunnen zijn, dat maakt niets uit.De standaard regel toepassen op de formule
F'(x) = f'(x) g(x) + f(x) g'(x). In de standaard regel zien we als eerste staan f(x). We hebben 3x net toegewezen aan de letter f. Het accent () achter letter f wijst erop dat dit moeten differentiëren. Als we 3x differentiëren houden we 3 over. We kunnen nu dus 3 invullen: F'(x) = 3 g(x) + f(x) g'(x).Nu zien we g(x) staan. De (x) heeft hier eigenlijk geen betekenis. We moeten alleen de g vervangen door 5x³. We hebben net namelijk de 5x³ toegewezen aan de g. We krijgen nu dus: F'(x) = 3 5x³ + f(x) g'(x).
Nu zien we f(x) staan. We doen nu eigenlijk hetzelfde als de stap hiervoor. Weer heeft de (x) hier eigenlijk geen betekenis. We moeten alleen de f vervangen door 3x. We hebben net namelijk ook de 3x toegewezen aan de f. We krijgen nu dus: F'(x) = 3 5x³ + 3x g'(x).
Tenslotte zien we nog g'(x). Hier moeten we dus de afgeleide van g invullen. Aan g hebben we 5x³ toegewezen. De afgeleide daarvan wordt berekend door de 3 die rechtsboven de x staat (de 3e macht) maal de 5 te doen. Dat is dus 3 5 en dat wordt 15. Vervolgens doet men dan nog de 3 rechtsboven de x (de 3e macht) min 1, dat wordt dus 2. De afgeleide van het stukje 5x³ is dus 15x². Dat vullen we in in de standaard formule voor g'(x). We krijgen dan: F'(x) = 3 5x³ + 3x 15x²
De wiskundige uitkomst van het voorbeeld
De afgeleide is dus F'(x) = 3 5x³ + 3x 15x². Dit kan eventueel nog korter geschreven worden, maar dat niet verplicht. Korter geschreven wordt de afgeleide: F'(x) = 15x³ + 45x³. Dat wordt dan weer F(x)= 60x³.Lastige wiskundige termen
In dit artikel worden een aantal wiskundige termen gebruikt. Soms lijkt dat ingewikkeld, daarom worden hier een aantal wiskundige termen uitgelegd.Vermenigvuldigen: Twee of meer getallen keer elkaar doen, bijvoorbeeld 5 x 3 = 15. Men vermenigvuldigd 5 met 3 en de uitkomst daarvan is 15.
Het product: De uitkomst van iets dat met elkaar vermenigvuldigd wordt. Dus in het voorbeeld hierboven is 15 het product.
De afgeleide: De afgeleide is een speciale formule die men af leidt van een originele formule. Met deze afgeleide formule kan men bijvoorbeeld het richtingscoëfficiënt of de toppen van de originele formule bepalen.
Differentiëren: Differentiëren betekendt gewoon de afgeleide van een formule berekenen.
Richtingscoëfficiënt: Een getal dat aangeeft hoe stijl een grafiek daalt of stijgt. Dit wordt ook wel helling getal of rc genoemd.
Toppen, maximum of minimum, extreme waarden: De hoogste punten van een grafiek worden met deze termen aangeduid.
Termen: Met termen worden in de wiskunde vaak getallen bedoeld.
F(x): Dit staat altijd voor een formule. Dat wat achter F(x) staat is de formule. De letter F kan ook vervangen worden door elke andere letter uit het alfabet. In dit geval heet de formule F(x).
F'(x): Dit staat altijd voor de afgeleide van de formule. Dat wat achter F'(x) is de afgeleide. De F geeft aan dat het om de afgeleide van de originele formule F(x) gaat. Heet de originele formule G(x), dan heet de afgeleide ook G(x).
' : Het accent geeft, net als hierboven bij F'(x), altijd aan dat het om de afgeleide gaat.
Het product: De uitkomst van iets dat met elkaar vermenigvuldigd wordt. Dus in het voorbeeld hierboven is 15 het product.
De afgeleide: De afgeleide is een speciale formule die men af leidt van een originele formule. Met deze afgeleide formule kan men bijvoorbeeld het richtingscoëfficiënt of de toppen van de originele formule bepalen.
Differentiëren: Differentiëren betekendt gewoon de afgeleide van een formule berekenen.
Richtingscoëfficiënt: Een getal dat aangeeft hoe stijl een grafiek daalt of stijgt. Dit wordt ook wel helling getal of rc genoemd.
Toppen, maximum of minimum, extreme waarden: De hoogste punten van een grafiek worden met deze termen aangeduid.
Termen: Met termen worden in de wiskunde vaak getallen bedoeld.
F(x): Dit staat altijd voor een formule. Dat wat achter F(x) staat is de formule. De letter F kan ook vervangen worden door elke andere letter uit het alfabet. In dit geval heet de formule F(x).
F'(x): Dit staat altijd voor de afgeleide van de formule. Dat wat achter F'(x) is de afgeleide. De F geeft aan dat het om de afgeleide van de originele formule F(x) gaat. Heet de originele formule G(x), dan heet de afgeleide ook G(x).
' : Het accent geeft, net als hierboven bij F'(x), altijd aan dat het om de afgeleide gaat.
© 2012 - 2024 Ruttger, het auteursrecht van dit artikel ligt bij de infoteur. Zonder toestemming is vermenigvuldiging verboden. Per 2021 gaat InfoNu verder als archief, artikelen worden nog maar beperkt geactualiseerd.
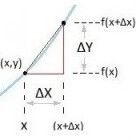 Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
Wiskunde de afgeleide en differentiërenDe afgeleide van een functie f(x) geeft ons informatie over hoe snel de functie stijgt of daalt in een zeker punt (x,y).…
 Goniometrische functies differentiëren en integrerenGoniometrische functies behandelen is een lastige zaak. Er moet met veel rekening worden gehouden, zoals of de functie e…
Goniometrische functies differentiëren en integrerenGoniometrische functies behandelen is een lastige zaak. Er moet met veel rekening worden gehouden, zoals of de functie e…
 Statistiek KansberekeningIn de statistiek gaat alles om de kans dat X gebeurt. Dit wordt ook wel kansrekening of waarschijnlijkheidsrekening geno…
Statistiek KansberekeningIn de statistiek gaat alles om de kans dat X gebeurt. Dit wordt ook wel kansrekening of waarschijnlijkheidsrekening geno…
 De Dr. Bibberregel in het schaatsenDe Dr. Bibberregel is een regel die moet voorkomend dat schaatsers op het rechte stuk de lijn overgaan met hun hele scha…
De Dr. Bibberregel in het schaatsenDe Dr. Bibberregel is een regel die moet voorkomend dat schaatsers op het rechte stuk de lijn overgaan met hun hele scha…
 Hoe kan ik de spelling van mijn kind extra oefenen?Naast rekenen en taal is spelling een belangrijk onderdeel binnen de schoolvaardigheden van je kind. Spelling werd vroeg…
Hoe kan ik de spelling van mijn kind extra oefenen?Naast rekenen en taal is spelling een belangrijk onderdeel binnen de schoolvaardigheden van je kind. Spelling werd vroeg…
 Welke factoren hebben invloed op het leren?In de loop van ons leven vergaren we veel kennis. De één meer dan de andere en de één lijkt het ook wat makkelijker af t…
Welke factoren hebben invloed op het leren?In de loop van ons leven vergaren we veel kennis. De één meer dan de andere en de één lijkt het ook wat makkelijker af t…
Gerelateerde artikelen
Ruttger (31 artikelen)
Gepubliceerd: 02-04-2012
Rubriek: Educatie en School
Subrubriek: Studievaardigheden
Gepubliceerd: 02-04-2012
Rubriek: Educatie en School
Subrubriek: Studievaardigheden
Per 2021 gaat InfoNu verder als archief. Het grote aanbod van artikelen blijft beschikbaar maar er worden geen nieuwe artikelen meer gepubliceerd en nog maar beperkt geactualiseerd, daardoor kunnen artikelen op bepaalde punten verouderd zijn. Reacties plaatsen bij artikelen is niet meer mogelijk.